Luonnossa on runsaasti spiraalikuvioita hurrikaaneista kukkiin ja käpyihin. Matematiikka on kuvioiden tiedettä, joten ei ole yllättävää, että spiraalit ovat inspiroineet matemaatikkoja vuosisatojen ajan. Yksi näistä spiraaleista on kultainen spiraali, jonka ajatellaan olevan eräänlainen koodi, joka säätelee maailmankaikkeuden arkkitehtuuria. Kultainen spiraali on laaja, kiehtova aihe, joka on ollut merkittävässä asemassarooli historiassa ja taideteoksissa.

Seuraavassa tarkastellaan kultaista spiraalia - sen alkuperää, merkityksiä ja merkitystä.

Mikä on kultainen spiraalisymboli?

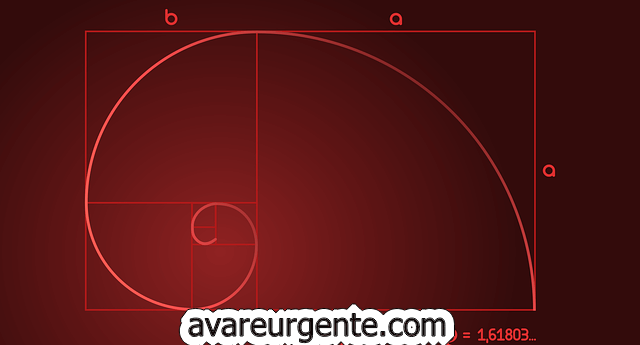
Kultainen spiraali on kuvio, joka perustuu kultaisen leikkauksen käsitteeseen - universaaliin lakiin, joka edustaa "ideaalia" kaikissa elämän ja aineen muodoissa. Itse asiassa se mainitaan usein esimerkkinä matematiikan lakien ja elävien olentojen rakenteen välisestä yhteydestä. Mitä enemmän ymmärrämme symbolin taustalla olevaa matematiikkaa, sitä enemmän arvostamme sen esiintymistä luonnossa ja taiteessa.

Matematiikassa kultainen leikkaus on erityinen luku, joka on suunnilleen yhtä suuri kuin 1,618 ja jota edustaa kreikkalainen kirjain Φ (Phi). Saatat ihmetellä, mistä tämä kultainen kierre tulee - ja vastaus siihen löytyy kultaisesta suorakulmiosta. Geometriassa kultainen kierre voidaan piirtää kultaisesta suorakulmiosta, jonka sivut on suhteutettu kultaisen leikkauksen mukaisesti.

1800-luvulla saksalainen matemaatikko Martin Ohm kutsui erikoislukua 1,618:ksi. kultainen , todennäköisesti siksi, että se on aina ollut olemassa matematiikassa. Vielä kauempana menneisyydessä sitä kuvattiin jopa nimellä jumalallinen Kultaisen leikkauksen perusteella syntyvää spiraalikuviota kutsutaan myös kultaiseksi leikkaukseksi. kultainen kierre.

Kultainen kierre vs. Fibonaccin kierre

Kultainen leikkaus esiintyy monissa matemaattisissa yhteyksissä. Siksi kultainen kierre yhdistetään usein Fibonaccin sarjaan - numerosarjaan, joka liittyy läheisesti Phi-lukuun. Teknisesti ottaen sarja alkaa luvuista 0 ja 1 ja jatkuu loputtomiin, ja jos jaat jokaisen luvun edeltäjällään, tulos on lähellä kultaista leikkausta, joka on noin 1,618.

Matematiikassa on useita spiraalikuvioita, ja niitä voidaan mitata. Kultainen spiraali ja Fibonaccin spiraali ovat muodoltaan hyvin samankaltaisia, ja monet käyttävät niitä vaihtamalla niitä keskenään, mutta ne eivät ole sama asia. Kaikki voidaan selittää matemaattisilla laskelmilla, eikä niillä ole samaa täsmällistä kuviota mitattuna.

Sanotaan, että Fibonaccin spiraali vastaa kultaista spiraalia vasta tietyssä vaiheessa, kun ensimmäinen lähestyy kultaista leikkausta eli 1,618. Itse asiassa mitä korkeammat Fibonaccin luvut ovat, sitä lähempänä niiden suhde on Phi:tä. Kannattaa muistaa, että kaikki luonnossa esiintyvät spiraalit eivät perustu Fibonaccin lukuihin tai kultaiseen leikkaukseen.

Kultaisen spiraalin merkitys ja symboliikka

Kultainen spiraalisymboli on inspiroinut lukemattomia ihmisiä kautta historian, ja se on yhdistetty elämän, henkisyyden ja luomisen perusasioihin.

• Elämä ja luominen

Kultainen kierre on ainutlaatuinen matemaattisilta ominaisuuksiltaan ja todistaa, että elämme matemaattisten lakien hallitsemassa maailmankaikkeudessa. Kun toiset uskovat, että se on vain hyvin outo sattuma, monet tiedemiehet ja tutkijat pitävät sitä todisteena mestarimatemaatikosta tai Luojasta. Loppujen lopuksi luonnon älykäs suunnittelu on monimutkaista, ja joistakin saattaa tuntua epäloogiselta ajatella, että se onsyntyi sattumalta.

• Tasapaino ja harmonia

Kultainen spiraali on kauneudellaan vanginnut matemaatikkojen, suunnittelijoiden ja taiteilijoiden mielikuvituksen. Se on heijastunut joihinkin suurimpiin taide- ja arkkitehtuuriteoksiin. Se on myös yhdistetty kauneuteen, sillä monet uskovat kauneuden keskittyvän sen ainutlaatuisiin ominaisuuksiin matematiikassa ja geometriassa. Jotkut mystikot uskovat, että symboli tuo myös tasapainoa ja harmoniaa elämään.

Kultainen spiraali symboli historiassa

Kultaisen spiraalin symbolin kiehtovuus on saanut monet taiteilijat käyttämään sitä mestariteoksissaan. On hyvin mahdollista, että olet jo nähnyt symbolin päällekkäisinä eri taidemuodoissa Parthenonista Mona Lisaan. Valitettavasti aiheesta on esitetty monia hämmentäviä väitteitä, joten autamme sinua päättämään, perustuvatko ne myyttiin vai matematiikkaan.

• Parthenon

Kreikan Ateenassa vuosina 447-438 eaa. rakennettu Parthenon on yksi kaikkien aikojen esteettisimmistä rakennelmista. Monet arvelevat, että se on rakennettu kultaisen leikkauksen perusteella. Näet jopa useita kuvauksia temppelin etujulkisivusta, joissa on kultainen kierre ja kultainen suorakulmio.

Ei ole epäilystäkään siitä, että antiikin kreikkalaiset sisällyttivät matematiikkaa ja geometriaa arkkitehtuuriinsa, mutta tutkijat eivät löydä konkreettisia todisteita siitä, että he olisivat käyttäneet kultaista leikkausta Parthenonin rakentamisessa. Monet pitävät sitä myyttinä, koska suurin osa matemaattisista lauseista kehitettiin vasta temppelin rakentamisen jälkeen.

Lisäksi tarvitaan tarkkoja mittauksia, jotta voidaan päätellä, että suunnittelussa käytettiin kultaista suhdelukua ja kultaista spiraalia. Asiantuntijoiden mukaan kultainen suorakulmio pitäisi kehystää Parthenonia lähestyvien portaiden juuressa, ei sen pylväiden juuressa - kuten useissa kuvissa on yleisesti esitetty. Rakennelma on myös raunioina, minkä vuoksi sen tarkat mitat ovat epävarmoja.arvio.

• Leonardo da Vincin maalaukset

Leonardo da Vinciä on pitkään pidetty kultaiseen leikkaukseen liittyvänä "jumalallisena" taidemaalarina. Tätä yhdistelmää tuki jopa romaani Da Vinci -koodi Vaikka kaikki on tulkinnanvaraista, monet ovat arvelleet, että taidemaalari käytti teoksissaan tarkoituksella kultaista kierrettä saavuttaakseen tasapainon ja kauneuden.

Da Vincin käyttämä kultainen leikkaus on ilmeinen teoksessa Viimeinen ehtoollinen ja The Annuciation , mutta Mona Lisa tai La Joconde on edelleen kiistanalainen. Sanotaan, että arkkitehtonisia elementtejä ja suoria linjoja, joita voisi käyttää vertailukohtina, on vähän verrattuna kahteen muuhun maalaukseen. Mona Lisasta löytyy silti useita kultaisen suhdeluvun tulkintoja, joissa kultainen spiraali on päällekkäin.

Emme luultavasti koskaan saa tietää Da Vincin tarkoitusta mestariteostensa suhteen, mutta monet pitävät outoa yhteensattumaa kiehtovana. Kun otetaan huomioon taidemaalarin aiempi käyttö, ei olisi odottamatonta, että hän olisi käyttänyt sitä myös kyseisessä maalauksessa. Kannattaa vain pitää mielessä, että kaikissa Da Vincin maalauksissa ei ole selkeitä todisteita kultaisen leikkauksen ja kultaisen spiraalin sisällyttämisestä, joten on vaikea päätellä, että kaikkihänen mestariteoksensa perustuvat niihin.

Kultainen kierre -symboli nykyaikana

Kultainen spiraali auttaa meitä ymmärtämään elämää ja maailmankaikkeutta. Seuraavassa on joitakin symbolia koskevia viimeaikaisia löytöjä:

• Matematiikassa

Kultaisella spiraalilla on merkitystä fraktaalien geometriassa, joka on monimutkainen kuvio, joka toistuu ikuisesti. Amerikkalainen matemaatikko Edmund Harriss tuli tunnetuksi kultaiseen spiraaliin perustuvasta fraktaalikäyrästään, joka tunnetaan nykyään nimellä Harrissin spiraali. Hänen sanotaan pyrkineen piirtämään esteettisesti houkuttelevan näköisiä haarautuvia spiraaleja, mutta hän päätyi matemaattisen prosessin avulla ainutlaatuiseen spiraaliin.

• Biomekaniikassa

Kultaisella spiraalilla uskotaan olevan kiehtova vaikutus ihmiskäden liikkeisiin. Anatomin mukaan ihmisen sormien liike noudattaa kultaisen spiraalin kaavaa. Löydät jopa kuvia puristetusta nyrkistä, jossa spiraalisymboli on päällekkäin.

• Suunnittelussa ja kokoonpanossa

Nykyään monet suunnittelijat asettavat kultaisen spiraalin symbolin kuvan päälle havainnollistamaan sen kultaisen leikkauksen mittasuhteita toivoen saavuttavansa visuaalista harmoniaa töissään. Jotkin nykyaikaiset logot ja kuvakkeet perustuvat niihin, joissa suunnittelijat soveltavat niin sanottua "suhdelukujen sisällä olevien suhteiden" käsitettä.

• Luonnossa

Luonto on täynnä spiraalimaisia kuvioita, mutta varsinaista kultaista spiraalia luonnosta löytyy harvoin. Mielenkiintoista on, että tutkijat ovat havainneet, että haukat lentävät kultaista spiraalia lähestyessään saalista, todennäköisesti siksi, että se on energiatehokas lentoreitti.

Vastoin yleistä uskomusta nautiluksen kuori ei ole kultainen kierre. Mitattuna ne eivät vastaisi toisiaan riippumatta siitä, miten ne on kohdistettu tai skaalattu. Kaikki nautiluksen kuoret eivät myöskään ole samanlaisia, sillä niiden muodoissa on vaihtelua ja puutteita.

Auringonkukkien ja käpytikkujen spiraalit ovat kauniita, mutta ne eivät ole kultaisia spiraaleja. Itse asiassa niiden spiraalit eivät edes kierrä keskipisteen ympäri, toisin kuin kultainen spiraali. Vaikka joissakin kukissa terälehtien lukumäärä vastaa Fibonaccin lukuja, löytyy useita poikkeuksia.

Asiantuntijat sanovat myös, että galaksin tai satunnaisen myrskypilven, joka sopii kultaisen spiraalin osaan, ei pitäisi olla johtopäätös siitä, että kaikki galaksit ja hurrikaanit perustuvat kultaiseen leikkaukseen.

Lyhyesti

Maailmankaikkeutemme on täynnä spiraaleja, joten ei ole yllättävää, että monet ovat kiinnostuneet niiden taustalla olevasta matematiikasta ja niiden merkityksistä. Taiteilijat ovat jo pitkään pitäneet kultaista spiraalia silmää miellyttävimpänä. Se on todellakin yksi luonnon inspiroivimmista kuvioista, joka voidaan muuntaa luoviksi taiteellisiksi ilmaisuiksi.