ਵਿਸ਼ਾ - ਸੂਚੀ
ਤੂਫਾਨਾਂ ਤੋਂ ਲੈ ਕੇ ਫੁੱਲਾਂ ਅਤੇ ਪਾਈਨਕੋਨਸ ਤੱਕ, ਕੁਦਰਤ ਵਿੱਚ ਸਪਿਰਲ ਪੈਟਰਨ ਭਰਪੂਰ ਹਨ। ਗਣਿਤ ਪੈਟਰਨਾਂ ਦਾ ਵਿਗਿਆਨ ਹੈ, ਇਸ ਲਈ ਇਹ ਕੋਈ ਹੈਰਾਨੀ ਦੀ ਗੱਲ ਨਹੀਂ ਹੈ ਕਿ ਸਪੀਰਲਾਂ ਨੇ ਸਦੀਆਂ ਤੋਂ ਗਣਿਤ ਵਿਗਿਆਨੀਆਂ ਨੂੰ ਪ੍ਰੇਰਿਤ ਕੀਤਾ ਹੈ। ਇਹਨਾਂ ਚੱਕਰਾਂ ਵਿੱਚੋਂ ਇੱਕ ਗੋਲਡਨ ਸਪਿਰਲ ਹੈ, ਜਿਸਨੂੰ ਇੱਕ ਕਿਸਮ ਦਾ ਕੋਡ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਜੋ ਬ੍ਰਹਿਮੰਡ ਦੇ ਆਰਕੀਟੈਕਚਰ ਨੂੰ ਨਿਯੰਤ੍ਰਿਤ ਕਰਦਾ ਹੈ। ਸੁਨਹਿਰੀ ਚੱਕਰ ਇੱਕ ਵਿਸ਼ਾਲ, ਦਿਲਚਸਪ ਵਿਸ਼ਾ ਹੈ ਜਿਸਨੇ ਇਤਿਹਾਸ ਅਤੇ ਕਲਾ ਦੇ ਕੰਮਾਂ ਵਿੱਚ ਇੱਕ ਪ੍ਰਮੁੱਖ ਭੂਮਿਕਾ ਨਿਭਾਈ ਹੈ।
ਸੁਨਹਿਰੀ ਚੱਕਰ - ਇਸਦੇ ਮੂਲ, ਅਰਥ ਅਤੇ ਮਹੱਤਤਾ 'ਤੇ ਇੱਕ ਝਾਤ ਇਹ ਹੈ।
ਗੋਲਡਨ ਸਪਾਇਰਲ ਸਿੰਬਲ ਕੀ ਹੈ?
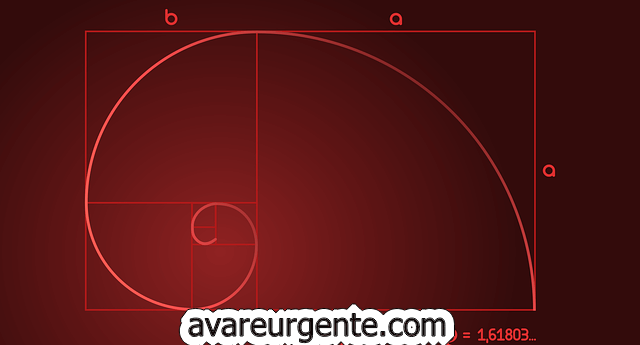
ਸੁਨਹਿਰੀ ਸਪਾਇਰਲ ਇੱਕ ਪੈਟਰਨ ਹੈ ਜੋ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਦੇ ਸੰਕਲਪ ਦੇ ਆਧਾਰ 'ਤੇ ਬਣਾਇਆ ਗਿਆ ਹੈ—ਇੱਕ ਵਿਸ਼ਵਵਿਆਪੀ ਨਿਯਮ ਜੋ ਜੀਵਨ ਅਤੇ ਪਦਾਰਥ ਦੇ ਸਾਰੇ ਰੂਪਾਂ ਵਿੱਚ "ਆਦਰਸ਼" ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ। ਵਾਸਤਵ ਵਿੱਚ, ਇਸਨੂੰ ਅਕਸਰ ਗਣਿਤ ਦੇ ਨਿਯਮਾਂ ਅਤੇ ਜੀਵਿਤ ਚੀਜ਼ਾਂ ਦੀ ਬਣਤਰ ਦੇ ਵਿਚਕਾਰ ਸਬੰਧ ਦੀ ਇੱਕ ਉਦਾਹਰਣ ਵਜੋਂ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ। ਜਿੰਨਾ ਜ਼ਿਆਦਾ ਅਸੀਂ ਪ੍ਰਤੀਕ ਦੇ ਪਿੱਛੇ ਦੇ ਗਣਿਤ ਨੂੰ ਸਮਝਾਂਗੇ, ਓਨਾ ਹੀ ਅਸੀਂ ਕੁਦਰਤ ਅਤੇ ਕਲਾਵਾਂ ਵਿੱਚ ਇਸਦੀ ਦਿੱਖ ਦੀ ਕਦਰ ਕਰਾਂਗੇ।
ਗਣਿਤ ਵਿੱਚ, ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸੰਖਿਆ ਹੈ ਜੋ ਲਗਭਗ 1.618 ਦੇ ਬਰਾਬਰ ਹੈ ਅਤੇ ਯੂਨਾਨੀ ਅੱਖਰ ਦੁਆਰਾ ਦਰਸਾਇਆ ਗਿਆ ਹੈ Φ (ਫਾਈ)। ਤੁਸੀਂ ਹੈਰਾਨ ਹੋ ਸਕਦੇ ਹੋ ਕਿ ਇਹ ਸੁਨਹਿਰੀ ਚੱਕਰ ਕਿੱਥੋਂ ਆਉਂਦਾ ਹੈ - ਅਤੇ ਇਸਦਾ ਜਵਾਬ ਸੁਨਹਿਰੀ ਆਇਤ ਦੇ ਅੰਦਰ ਹੈ। ਜਿਓਮੈਟਰੀ ਵਿੱਚ, ਸੁਨਹਿਰੀ ਚੱਕਰ ਇੱਕ ਸੁਨਹਿਰੀ ਆਇਤ ਤੋਂ ਖਿੱਚਿਆ ਜਾ ਸਕਦਾ ਹੈ ਜਿਸਦੇ ਪਾਸਿਆਂ ਨੂੰ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਅਨੁਸਾਰ ਅਨੁਪਾਤਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।
1800 ਵਿੱਚ, ਜਰਮਨ ਗਣਿਤ-ਸ਼ਾਸਤਰੀ ਮਾਰਟਿਨ ਓਹਮ ਨੇਵਿਸ਼ੇਸ਼ ਨੰਬਰ 1.618 ਸੁਨਹਿਰੀ , ਸੰਭਾਵਤ ਤੌਰ 'ਤੇ ਕਿਉਂਕਿ ਇਹ ਹਮੇਸ਼ਾ ਗਣਿਤ ਵਿੱਚ ਮੌਜੂਦ ਹੈ। ਸਮੇਂ ਦੇ ਅੱਗੇ, ਇਸਨੂੰ ਕੁਦਰਤੀ ਸੰਸਾਰ ਵਿੱਚ ਇਸਦੀ ਬਾਰੰਬਾਰਤਾ ਦੇ ਕਾਰਨ ਬ੍ਰਹਮ ਵਜੋਂ ਵੀ ਦਰਸਾਇਆ ਗਿਆ ਸੀ। ਗੋਲਡਨ ਰੇਸ਼ੋ ਤੋਂ ਬਣਾਏ ਗਏ ਸਪਿਰਲ ਪੈਟਰਨ ਨੂੰ ਗੋਲਡਨ ਸਪਾਈਰਲ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਗੋਲਡਨ ਸਪਾਈਰਲ ਬਨਾਮ ਫਿਬੋਨਾਚੀ ਸਪਾਈਰਲ

ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਕਈਆਂ ਵਿੱਚ ਹੁੰਦਾ ਹੈ। ਗਣਿਤ ਦੇ ਸੰਦਰਭ ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਸੁਨਹਿਰੀ ਸਪਿਰਲ ਅਕਸਰ ਫਿਬੋਨਾਚੀ ਕ੍ਰਮ ਨਾਲ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ - ਫਾਈ ਨਾਲ ਨੇੜਿਓਂ ਜੁੜੀਆਂ ਸੰਖਿਆਵਾਂ ਦੀ ਇੱਕ ਲੜੀ। ਤਕਨੀਕੀ ਤੌਰ 'ਤੇ, ਕ੍ਰਮ 0 ਅਤੇ 1 ਨਾਲ ਸ਼ੁਰੂ ਹੁੰਦਾ ਹੈ ਅਤੇ ਅਨੰਤ ਤੌਰ 'ਤੇ ਜਾਰੀ ਰਹਿੰਦਾ ਹੈ, ਅਤੇ ਜੇਕਰ ਤੁਸੀਂ ਹਰੇਕ ਸੰਖਿਆ ਨੂੰ ਇਸਦੇ ਪੂਰਵ ਸੰਖਿਆ ਨਾਲ ਵੰਡਦੇ ਹੋ, ਤਾਂ ਨਤੀਜਾ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ, ਲਗਭਗ 1.618 ਵਿੱਚ ਬਦਲ ਜਾਵੇਗਾ।
ਗਣਿਤ ਵਿੱਚ, ਕਈ ਚੱਕਰੀ ਪੈਟਰਨ ਹਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਾਪਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਗੋਲਡਨ ਸਪਾਇਰਲ ਅਤੇ ਫਿਬੋਨਾਚੀ ਸਪਿਰਲ ਆਕਾਰ ਵਿੱਚ ਬਹੁਤ ਸਮਾਨ ਹਨ, ਅਤੇ ਬਹੁਤ ਸਾਰੇ ਇਹਨਾਂ ਨੂੰ ਇੱਕ ਦੂਜੇ ਦੇ ਬਦਲੇ ਵਰਤਦੇ ਹਨ, ਪਰ ਉਹ ਇੱਕੋ ਜਿਹੇ ਨਹੀਂ ਹਨ। ਹਰ ਚੀਜ਼ ਨੂੰ ਗਣਿਤਿਕ ਗਣਨਾਵਾਂ ਦੁਆਰਾ ਸਮਝਾਇਆ ਜਾ ਸਕਦਾ ਹੈ, ਅਤੇ ਮਾਪਣ 'ਤੇ ਉਹਨਾਂ ਦਾ ਉਹੀ ਸਹੀ ਪੈਟਰਨ ਨਹੀਂ ਹੋਵੇਗਾ।
ਇਹ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਫਿਬੋਨਾਚੀ ਸਪਿਰਲ ਸਿਰਫ਼ ਇੱਕ ਨਿਸ਼ਚਿਤ ਬਿੰਦੂ 'ਤੇ ਸੁਨਹਿਰੀ ਸਪਿਰਲ ਨਾਲ ਮੇਲ ਖਾਂਦਾ ਹੈ, ਜਦੋਂ ਪਹਿਲਾ ਗੋਲਡਨ ਅਨੁਪਾਤ ਤੱਕ ਪਹੁੰਚਦਾ ਹੈ ਜਾਂ 1.618। ਵਾਸਤਵ ਵਿੱਚ, ਫਿਬੋਨਾਚੀ ਨੰਬਰ ਜਿੰਨੇ ਉੱਚੇ ਹਨ, ਉਹਨਾਂ ਦਾ ਫਾਈ ਨਾਲ ਰਿਸ਼ਤਾ ਓਨਾ ਹੀ ਨੇੜੇ ਹੈ। ਬਸ ਇਹ ਗੱਲ ਧਿਆਨ ਵਿੱਚ ਰੱਖੋ ਕਿ ਕੁਦਰਤ ਵਿੱਚ ਪਾਇਆ ਜਾਣ ਵਾਲਾ ਹਰ ਚੱਕਰ ਫਿਬੋਨਾਚੀ ਨੰਬਰਾਂ ਜਾਂ ਸੁਨਹਿਰੀ 'ਤੇ ਆਧਾਰਿਤ ਨਹੀਂ ਹੈਅਨੁਪਾਤ।
ਗੋਲਡਨ ਸਪਿਰਲ ਦਾ ਅਰਥ ਅਤੇ ਪ੍ਰਤੀਕਵਾਦ
ਸੁਨਹਿਰੀ ਸਪਾਈਰਲ ਪ੍ਰਤੀਕ ਨੇ ਪੂਰੇ ਇਤਿਹਾਸ ਵਿੱਚ ਅਣਗਿਣਤ ਲੋਕਾਂ ਨੂੰ ਪ੍ਰੇਰਿਤ ਕੀਤਾ ਹੈ। ਇਹ ਜੀਵਨ, ਅਧਿਆਤਮਿਕਤਾ ਅਤੇ ਸ੍ਰਿਸ਼ਟੀ ਦੇ ਬੁਨਿਆਦੀ ਤੱਤਾਂ ਨਾਲ ਜੁੜਿਆ ਹੋਇਆ ਹੈ।
- ਜੀਵਨ ਅਤੇ ਸ੍ਰਿਸ਼ਟੀ
ਸੁਨਹਿਰੀ ਚੱਕਰ ਇਸਦੀਆਂ ਗਣਿਤਿਕ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਵਿੱਚ ਵਿਲੱਖਣ ਹੈ ਅਤੇ ਇਹ ਸਾਬਤ ਕਰਦਾ ਹੈ ਕਿ ਅਸੀਂ ਗਣਿਤ ਦੇ ਨਿਯਮਾਂ ਦੁਆਰਾ ਨਿਯੰਤਰਿਤ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਰਹਿੰਦੇ ਹਾਂ। ਜਦੋਂ ਕਿ ਦੂਸਰੇ ਮੰਨਦੇ ਹਨ ਕਿ ਇਹ ਸਿਰਫ ਇੱਕ ਬਹੁਤ ਹੀ ਅਜੀਬ ਇਤਫ਼ਾਕ ਹੈ, ਬਹੁਤ ਸਾਰੇ ਵਿਗਿਆਨੀ ਅਤੇ ਖੋਜਕਰਤਾ ਇਸਨੂੰ ਇੱਕ ਮਾਸਟਰ ਗਣਿਤ-ਸ਼ਾਸਤਰੀ ਜਾਂ ਇੱਕ ਸਿਰਜਣਹਾਰ ਦਾ ਸਬੂਤ ਮੰਨਦੇ ਹਨ। ਆਖ਼ਰਕਾਰ, ਕੁਦਰਤ ਵਿੱਚ ਬੁੱਧੀਮਾਨ ਡਿਜ਼ਾਈਨ ਗੁੰਝਲਦਾਰ ਹੈ, ਅਤੇ ਕੁਝ ਲੋਕਾਂ ਲਈ ਇਹ ਸੋਚਣਾ ਤਰਕਹੀਣ ਜਾਪਦਾ ਹੈ ਕਿ ਇਹ ਸੰਜੋਗ ਨਾਲ ਹੋਇਆ ਹੈ।
- ਸੰਤੁਲਨ ਅਤੇ ਸਦਭਾਵਨਾ <1
- The Parthenon
- ਲਿਓਨਾਰਡੋ ਦਾ ਵਿੰਚੀ ਦੀਆਂ ਪੇਂਟਿੰਗਾਂ
- ਗਣਿਤ ਵਿੱਚ
- ਬਾਇਓਮੈਕਨਿਕਸ ਵਿੱਚ
- ਡਿਜ਼ਾਇਨ ਅਤੇ ਰਚਨਾ ਵਿੱਚ
- ਕੁਦਰਤ ਵਿੱਚ
ਸੁਨਹਿਰੀ ਚੱਕਰ ਨੇ ਆਪਣੀ ਸੁੰਦਰਤਾ ਨਾਲ ਗਣਿਤ ਵਿਗਿਆਨੀਆਂ, ਡਿਜ਼ਾਈਨਰਾਂ ਅਤੇ ਕਲਾਕਾਰਾਂ ਦੀ ਕਲਪਨਾ ਨੂੰ ਆਪਣੇ ਵੱਲ ਖਿੱਚ ਲਿਆ ਹੈ। ਇਹ ਕਲਾ ਅਤੇ ਆਰਕੀਟੈਕਚਰ ਦੇ ਕੁਝ ਮਹਾਨ ਕੰਮਾਂ ਵਿੱਚ ਝਲਕਦਾ ਹੈ। ਇਹ ਸੁੰਦਰਤਾ ਨਾਲ ਵੀ ਜੁੜਿਆ ਹੋਇਆ ਹੈ, ਕਿਉਂਕਿ ਬਹੁਤ ਸਾਰੇ ਮੰਨਦੇ ਹਨ ਕਿ ਸੁੰਦਰਤਾ ਗਣਿਤ ਅਤੇ ਜਿਓਮੈਟਰੀ ਵਿੱਚ ਇਸਦੇ ਵਿਲੱਖਣ ਗੁਣਾਂ 'ਤੇ ਕੇਂਦਰਿਤ ਹੈ। ਕੁਝ ਰਹੱਸਵਾਦੀ ਮੰਨਦੇ ਹਨ ਕਿ ਇਹ ਪ੍ਰਤੀਕ ਕਿਸੇ ਦੇ ਜੀਵਨ ਵਿੱਚ ਸੰਤੁਲਨ ਅਤੇ ਸਦਭਾਵਨਾ ਵੀ ਲਿਆਏਗਾ।
ਇਤਿਹਾਸ ਵਿੱਚ ਗੋਲਡਨ ਸਪਾਈਰਲ ਸਿੰਬਲ
ਸੁਨਹਿਰੀ ਸਪਿਰਲ ਪ੍ਰਤੀਕ ਦੇ ਨਾਲ ਮੋਹ ਨੇ ਬਹੁਤ ਸਾਰੇ ਕਲਾਕਾਰਾਂ ਨੂੰ ਇਸਦੀ ਵਰਤੋਂ ਕਰਨ ਲਈ ਪ੍ਰੇਰਿਤ ਕੀਤਾ ਹੈ। ਮਾਸਟਰਪੀਸ ਇੱਥੇ ਇੱਕ ਵਧੀਆ ਮੌਕਾ ਹੈ ਕਿ ਤੁਸੀਂ ਪਹਿਲਾਂ ਹੀ ਪ੍ਰਤੀਕ ਨੂੰ ਵੱਖ-ਵੱਖ ਕਲਾ 'ਤੇ ਓਵਰਲੇਅ ਵਜੋਂ ਦੇਖਿਆ ਹੈਰੂਪ, ਪਾਰਥੇਨਨ ਤੋਂ ਮੋਨਾ ਲੀਸਾ ਤੱਕ। ਬਦਕਿਸਮਤੀ ਨਾਲ, ਵਿਸ਼ੇ ਬਾਰੇ ਬਹੁਤ ਸਾਰੇ ਭੰਬਲਭੂਸੇ ਵਾਲੇ ਦਾਅਵੇ ਹਨ, ਇਸਲਈ ਅਸੀਂ ਇਹ ਫੈਸਲਾ ਕਰਨ ਵਿੱਚ ਤੁਹਾਡੀ ਮਦਦ ਕਰਾਂਗੇ ਕਿ ਉਹ ਮਿਥਿਹਾਸ ਜਾਂ ਗਣਿਤ ਵਿੱਚ ਆਧਾਰਿਤ ਹਨ।

447 ਅਤੇ 438 ਈਸਵੀ ਪੂਰਵ ਦੇ ਵਿਚਕਾਰ ਬਣਾਇਆ ਗਿਆ, ਏਥਨਜ਼, ਗ੍ਰੀਸ ਵਿੱਚ ਪਾਰਥੇਨਨ ਹੁਣ ਤੱਕ ਬਣਾਈਆਂ ਗਈਆਂ ਸਭ ਤੋਂ ਸੁਹਜਾਤਮਕ ਤੌਰ 'ਤੇ ਮਨਮੋਹਕ ਬਣਤਰਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ। ਬਹੁਤ ਸਾਰੇ ਅਨੁਮਾਨ ਲਗਾਉਂਦੇ ਹਨ ਕਿ ਇਹ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਦੇ ਅਧਾਰ ਤੇ ਬਣਾਇਆ ਗਿਆ ਸੀ. ਤੁਸੀਂ ਮੰਦਰ ਦੇ ਅਗਲੇ ਹਿੱਸੇ ਦੇ ਕਈ ਚਿੱਤਰ ਵੀ ਦੇਖੋਗੇ ਜਿਸ 'ਤੇ ਸੁਨਹਿਰੀ ਚੱਕਰ ਅਤੇ ਸੁਨਹਿਰੀ ਆਇਤਕਾਰ ਹੈ।
ਇਸ ਵਿੱਚ ਕੋਈ ਸ਼ੱਕ ਨਹੀਂ ਹੈ ਕਿ ਪ੍ਰਾਚੀਨ ਯੂਨਾਨੀਆਂ ਨੇ ਆਪਣੀ ਆਰਕੀਟੈਕਚਰ ਵਿੱਚ ਗਣਿਤ ਅਤੇ ਜਿਓਮੈਟਰੀ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਸੀ, ਪਰ ਵਿਦਵਾਨ ਅਜਿਹਾ ਨਹੀਂ ਕਰ ਸਕਦੇ। ਠੋਸ ਸਬੂਤ ਲੱਭੋ ਕਿ ਉਨ੍ਹਾਂ ਨੇ ਪਾਰਥੇਨਨ ਬਣਾਉਣ ਵਿਚ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਸੀ। ਬਹੁਤ ਸਾਰੇ ਲੋਕ ਇਸਨੂੰ ਇੱਕ ਮਿੱਥ ਸਮਝਦੇ ਹਨ ਕਿਉਂਕਿ ਜ਼ਿਆਦਾਤਰ ਗਣਿਤਿਕ ਸਿਧਾਂਤ ਮੰਦਰ ਦੇ ਨਿਰਮਾਣ ਤੋਂ ਬਾਅਦ ਹੀ ਵਿਕਸਤ ਕੀਤੇ ਗਏ ਸਨ।
ਹੋਰ ਕੀ ਹੈ, ਇਹ ਸਿੱਟਾ ਕੱਢਣ ਲਈ ਕਿ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਅਤੇ ਸੁਨਹਿਰੀ ਸਪਿਰਲ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਗਈ ਸੀ, ਸਹੀ ਮਾਪਾਂ ਦੀ ਲੋੜ ਹੈ। ਡਿਜ਼ਾਈਨ. ਮਾਹਰਾਂ ਦੇ ਅਨੁਸਾਰ, ਸੁਨਹਿਰੀ ਆਇਤਕਾਰ ਨੂੰ ਪਾਰਥੇਨਨ ਦੇ ਨੇੜੇ ਆਉਣ ਵਾਲੇ ਕਦਮਾਂ ਦੇ ਅਧਾਰ 'ਤੇ ਬਣਾਇਆ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ, ਨਾ ਕਿ ਇਸਦੇ ਕਾਲਮਾਂ ਦੇ ਅਧਾਰ 'ਤੇ - ਜਿਵੇਂ ਕਿ ਆਮ ਤੌਰ 'ਤੇ ਕਈ ਚਿੱਤਰਾਂ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਨਾਲ ਹੀ, ਢਾਂਚਾ ਖੰਡਰ ਵਿੱਚ ਹੈ, ਜੋ ਇਸਦੇ ਸਹੀ ਮਾਪਾਂ ਨੂੰ ਕੁਝ ਅੰਦਾਜ਼ੇ ਦੇ ਅਧੀਨ ਬਣਾਉਂਦਾ ਹੈ।

ਲਿਓਨਾਰਡੋ ਦਾ ਵਿੰਚੀ ਨੂੰ ਲੰਬੇ ਸਮੇਂ ਤੋਂ "ਬ੍ਰਹਮ" ਕਿਹਾ ਜਾਂਦਾ ਰਿਹਾ ਹੈਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਨਾਲ ਸਬੰਧਤ ਚਿੱਤਰਕਾਰ. ਇਸ ਸਬੰਧ ਨੂੰ ਨਾਵਲ ਦਾ ਵਿੰਚੀ ਕੋਡ ਦੁਆਰਾ ਵੀ ਸਮਰਥਨ ਦਿੱਤਾ ਗਿਆ ਸੀ, ਕਿਉਂਕਿ ਪਲਾਟ ਵਿੱਚ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਅਤੇ ਫਿਬੋਨਾਚੀ ਸੰਖਿਆਵਾਂ ਸ਼ਾਮਲ ਹਨ। ਹਾਲਾਂਕਿ ਸਭ ਕੁਝ ਵਿਆਖਿਆ ਦੇ ਅਧੀਨ ਹੈ, ਕਈਆਂ ਨੇ ਅਨੁਮਾਨ ਲਗਾਇਆ ਹੈ ਕਿ ਚਿੱਤਰਕਾਰ ਨੇ ਜਾਣਬੁੱਝ ਕੇ ਸੰਤੁਲਨ ਅਤੇ ਸੁੰਦਰਤਾ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਆਪਣੀਆਂ ਰਚਨਾਵਾਂ ਵਿੱਚ ਸੁਨਹਿਰੀ ਚੱਕਰ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਹੈ।
ਦਾ ਵਿੰਚੀ ਦੁਆਰਾ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਦੀ ਵਰਤੋਂ ਦ ਲਾਸਟ ਸਪਰ<ਵਿੱਚ ਸਪੱਸ਼ਟ ਹੈ। 8. ਇਹ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਦੂਜੀਆਂ ਦੋ ਪੇਂਟਿੰਗਾਂ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਸੰਦਰਭ ਬਿੰਦੂਆਂ ਦੇ ਤੌਰ 'ਤੇ ਵਰਤੇ ਜਾਣ ਲਈ ਕੁਝ ਆਰਕੀਟੈਕਚਰਲ ਤੱਤ ਅਤੇ ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਹਨ। ਫਿਰ ਵੀ, ਤੁਸੀਂ ਮੋਨਾ ਲੀਸਾ 'ਤੇ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਦੀਆਂ ਕਈ ਵਿਆਖਿਆਵਾਂ ਲੱਭ ਸਕਦੇ ਹੋ, ਜਿਸ ਵਿੱਚ ਸੁਨਹਿਰੀ ਸਪਿਰਲ ਨੂੰ ਓਵਰਲੇਅ ਵਜੋਂ ਦਰਸਾਇਆ ਗਿਆ ਹੈ।
ਅਸੀਂ ਸ਼ਾਇਦ ਕਦੇ ਵੀ ਦਾ ਵਿੰਚੀ ਦੇ ਉਸਦੀਆਂ ਮਾਸਟਰਪੀਸ ਲਈ ਇਰਾਦੇ ਨੂੰ ਨਹੀਂ ਜਾਣ ਸਕਾਂਗੇ, ਪਰ ਕਈਆਂ ਨੂੰ ਅਜੀਬ ਇਤਫ਼ਾਕ ਨੂੰ ਮਜਬੂਰ ਕਰਨ ਵਾਲਾ ਲੱਗਦਾ ਹੈ। ਪੇਂਟਰ ਦੀ ਪੂਰਵ ਵਰਤੋਂ ਨੂੰ ਦੇਖਦੇ ਹੋਏ, ਉਸ ਲਈ ਉਕਤ ਪੇਂਟਿੰਗ 'ਤੇ ਵੀ ਇਸ ਦੀ ਵਰਤੋਂ ਕਰਨਾ ਅਚਾਨਕ ਨਹੀਂ ਹੋਵੇਗਾ। ਬਸ ਇਹ ਗੱਲ ਧਿਆਨ ਵਿੱਚ ਰੱਖੋ ਕਿ ਹਰ ਦਾ ਵਿੰਚੀ ਦੀ ਪੇਂਟਿੰਗ ਵਿੱਚ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਅਤੇ ਸੁਨਹਿਰੀ ਸਪਿਰਲ ਦੇ ਸ਼ਾਮਲ ਹੋਣ ਦਾ ਸਪੱਸ਼ਟ ਸਬੂਤ ਨਹੀਂ ਹੈ, ਇਸ ਲਈ ਇਹ ਸਿੱਟਾ ਕੱਢਣਾ ਮੁਸ਼ਕਲ ਹੈ ਕਿ ਉਸ ਦੀਆਂ ਸਾਰੀਆਂ ਮਾਸਟਰਪੀਸ ਉਹਨਾਂ 'ਤੇ ਆਧਾਰਿਤ ਹਨ।
ਗੋਲਡਨ ਸਪਾਈਰਲ ਸਿੰਬਲ ਵਿੱਚ ਆਧੁਨਿਕ ਸਮਾਂ
ਸੁਨਹਿਰੀ ਚੱਕਰ ਸਾਡੀ ਜ਼ਿੰਦਗੀ ਅਤੇ ਬ੍ਰਹਿਮੰਡ ਦੀ ਸਮਝ ਵਿੱਚ ਯੋਗਦਾਨ ਪਾਉਂਦਾ ਹੈ। ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਕੁਝ ਤਾਜ਼ਾ ਖੋਜਾਂ ਇੱਥੇ ਹਨਚਿੰਨ੍ਹ:
ਸੁਨਹਿਰੀ ਸਪਿਰਲ ਫਰੈਕਟਲ ਦੀ ਜਿਓਮੈਟਰੀ ਵਿੱਚ ਇੱਕ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦਾ ਹੈ, ਇੱਕ ਗੁੰਝਲਦਾਰ ਪੈਟਰਨ ਜੋ ਹਮੇਸ਼ਾ ਲਈ ਦੁਹਰਾਇਆ ਜਾਂਦਾ ਹੈ। ਅਮਰੀਕੀ ਗਣਿਤ-ਵਿਗਿਆਨੀ ਐਡਮੰਡ ਹੈਰਿਸ ਸੁਨਹਿਰੀ ਸਪਿਰਲ 'ਤੇ ਆਧਾਰਿਤ ਆਪਣੇ ਫ੍ਰੈਕਟਲ ਕਰਵ ਲਈ ਪ੍ਰਸਿੱਧ ਹੋਇਆ, ਜਿਸ ਨੂੰ ਹੁਣ ਹੈਰਿਸ ਸਪਾਈਰਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਉਸਦਾ ਉਦੇਸ਼ ਸ਼ਾਖਾਵਾਂ ਦੇ ਚੱਕਰਾਂ ਨੂੰ ਖਿੱਚਣਾ ਸੀ ਜੋ ਸੁਹਜ ਦੇ ਰੂਪ ਵਿੱਚ ਆਕਰਸ਼ਕ ਦਿਖਾਈ ਦਿੰਦੇ ਹਨ, ਪਰ ਉਸਨੇ ਇੱਕ ਗਣਿਤਿਕ ਪ੍ਰਕਿਰਿਆ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਇੱਕ ਵਿਲੱਖਣ ਸਪਿਰਲ ਨਾਲ ਸਮਾਪਤ ਕੀਤਾ।
ਸੁਨਹਿਰੀ ਚੱਕਰ ਮਨੁੱਖੀ ਹੱਥ ਦੀ ਗਤੀ ਉੱਤੇ ਇੱਕ ਦਿਲਚਸਪ ਪ੍ਰਭਾਵ ਰੱਖਣ ਲਈ ਸੋਚਿਆ ਜਾਂਦਾ ਹੈ। ਇੱਕ ਸਰੀਰ ਵਿਗਿਆਨੀ ਦੇ ਅਨੁਸਾਰ, ਮਨੁੱਖੀ ਉਂਗਲਾਂ ਦੀ ਗਤੀ ਸੋਨੇ ਦੇ ਚੱਕਰ ਦੇ ਨਮੂਨੇ ਦੀ ਪਾਲਣਾ ਕਰਦੀ ਹੈ. ਤੁਹਾਨੂੰ ਓਵਰਲੇਅ ਦੇ ਰੂਪ ਵਿੱਚ ਸਪਿਰਲ ਚਿੰਨ੍ਹ ਦੇ ਨਾਲ ਇੱਕ ਕਲੰਚ ਕੀਤੀ ਮੁੱਠੀ ਦੀਆਂ ਤਸਵੀਰਾਂ ਵੀ ਮਿਲਣਗੀਆਂ।
ਅੱਜ-ਕੱਲ੍ਹ, ਬਹੁਤ ਸਾਰੇ ਡਿਜ਼ਾਈਨਰ ਓਵਰਲੇਅ ਕਰਦੇ ਹਨ ਉਹਨਾਂ ਦੇ ਕੰਮਾਂ ਵਿੱਚ ਵਿਜ਼ੂਅਲ ਇਕਸੁਰਤਾ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਉਮੀਦ ਵਿੱਚ ਇਸਦੇ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ ਦੇ ਅਨੁਪਾਤ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਇੱਕ ਚਿੱਤਰ ਉੱਤੇ ਇੱਕ ਸੁਨਹਿਰੀ ਚੱਕਰੀ ਚਿੰਨ੍ਹ। ਕੁਝ ਆਧੁਨਿਕ ਲੋਗੋ ਅਤੇ ਆਈਕਨ ਉਹਨਾਂ 'ਤੇ ਆਧਾਰਿਤ ਹਨ, ਜਿੱਥੇ ਡਿਜ਼ਾਈਨਰ "ਅਨੁਪਾਤ ਦੇ ਅੰਦਰ ਅਨੁਪਾਤ" ਦੀ ਅਖੌਤੀ ਧਾਰਨਾ ਨੂੰ ਲਾਗੂ ਕਰਦੇ ਹਨ।
ਕੁਦਰਤ ਚੱਕਰੀ ਪੈਟਰਨਾਂ ਨਾਲ ਭਰੀ ਹੋਈ ਹੈ ਪਰ ਕੁਦਰਤ ਵਿੱਚ ਅਸਲ ਸੁਨਹਿਰੀ ਚੱਕਰ ਲੱਭਣਾ ਬਹੁਤ ਘੱਟ ਹੈ। ਦਿਲਚਸਪ ਗੱਲ ਇਹ ਹੈ ਕਿ, ਵਿਗਿਆਨੀਆਂ ਨੇ ਇਹ ਪਤਾ ਲਗਾਇਆ ਹੈ ਕਿ ਬਾਜ਼ ਆਪਣੇ ਸ਼ਿਕਾਰ ਦੇ ਨੇੜੇ ਪਹੁੰਚਣ ਵੇਲੇ ਇੱਕ ਸੁਨਹਿਰੀ ਚੱਕਰੀ ਵਾਲੇ ਰਸਤੇ ਵਿੱਚ ਉੱਡਦੇ ਹਨ, ਸੰਭਾਵਤ ਤੌਰ 'ਤੇ ਕਿਉਂਕਿ ਇਹ ਊਰਜਾ-ਕੁਸ਼ਲ ਉਡਾਣ ਮਾਰਗ ਹੈ।
ਇਸ ਦੇ ਉਲਟਪ੍ਰਸਿੱਧ ਵਿਸ਼ਵਾਸ, ਨਟੀਲਸ ਸ਼ੈੱਲ ਇੱਕ ਸੁਨਹਿਰੀ ਚੱਕਰ ਨਹੀਂ ਹੈ। ਜਦੋਂ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਦੋਵੇਂ ਮੇਲ ਨਹੀਂ ਖਾਂਦੇ ਭਾਵੇਂ ਉਹਨਾਂ ਨੂੰ ਕਿਵੇਂ ਇਕਸਾਰ ਜਾਂ ਸਕੇਲ ਕੀਤਾ ਗਿਆ ਹੋਵੇ। ਨਾਲ ਹੀ, ਹਰੇਕ ਨਟੀਲਸ ਸ਼ੈੱਲ ਨੂੰ ਬਰਾਬਰ ਨਹੀਂ ਬਣਾਇਆ ਜਾਂਦਾ, ਕਿਉਂਕਿ ਹਰੇਕ ਵਿੱਚ ਆਕਾਰਾਂ ਵਿੱਚ ਭਿੰਨਤਾਵਾਂ ਅਤੇ ਅਪੂਰਣਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ।
ਸੂਰਜਮੁਖੀ ਅਤੇ ਪਾਈਨਕੋਨਸ ਦੇ ਚੱਕਰ ਬਹੁਤ ਸੁੰਦਰ ਹੁੰਦੇ ਹਨ, ਪਰ ਉਹ ਸੁਨਹਿਰੀ ਚੱਕਰ ਨਹੀਂ ਹੁੰਦੇ। ਵਾਸਤਵ ਵਿੱਚ, ਸੁਨਹਿਰੀ ਚੱਕਰ ਦੇ ਉਲਟ, ਉਹਨਾਂ ਦੇ ਚੱਕਰ ਕੇਂਦਰ ਦੇ ਦੁਆਲੇ ਵੀ ਨਹੀਂ ਲਪੇਟਦੇ ਹਨ। ਹਾਲਾਂਕਿ ਕੁਝ ਫੁੱਲਾਂ ਵਿੱਚ ਫਿਬੋਨਾਚੀ ਸੰਖਿਆਵਾਂ ਨਾਲ ਮੇਲ ਖਾਂਦੀਆਂ ਪੱਤੀਆਂ ਦੀ ਗਿਣਤੀ ਹੁੰਦੀ ਹੈ, ਕਈ ਅਪਵਾਦ ਪਾਏ ਜਾਂਦੇ ਹਨ।
ਮਾਹਰ ਇਹ ਵੀ ਕਹਿੰਦੇ ਹਨ ਕਿ ਇੱਕ ਗਲੈਕਸੀ ਜਾਂ ਕਦੇ-ਕਦਾਈਂ ਤੂਫ਼ਾਨ ਦਾ ਬੱਦਲ ਜੋ ਕਿ ਇੱਕ ਸੁਨਹਿਰੀ ਚੱਕਰ ਦੇ ਇੱਕ ਹਿੱਸੇ ਵਿੱਚ ਫਿੱਟ ਹੁੰਦਾ ਹੈ, ਇੱਕ ਸਿੱਟਾ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਸਾਰੀਆਂ ਗਲੈਕਸੀਆਂ ਅਤੇ ਤੂਫ਼ਾਨ ਸੁਨਹਿਰੀ ਅਨੁਪਾਤ 'ਤੇ ਅਧਾਰਤ ਹਨ।
ਸੰਖੇਪ ਵਿੱਚ
ਸਾਡਾ ਬ੍ਰਹਿਮੰਡ ਚੱਕਰਾਂ ਨਾਲ ਭਰਿਆ ਹੋਇਆ ਹੈ, ਇਸ ਲਈ ਇਹ ਕੋਈ ਹੈਰਾਨੀ ਦੀ ਗੱਲ ਨਹੀਂ ਹੈ ਕਿ ਬਹੁਤ ਸਾਰੇ ਲੋਕਾਂ ਨੂੰ ਉਹਨਾਂ ਦੇ ਪਿੱਛੇ ਦੇ ਗਣਿਤ ਅਤੇ ਉਹਨਾਂ ਦੇ ਅਰਥਾਂ ਵਿੱਚ ਦਿਲਚਸਪੀ ਹੋ ਗਈ ਹੈ . ਕਲਾਕਾਰਾਂ ਨੇ ਲੰਬੇ ਸਮੇਂ ਤੋਂ ਸੁਨਹਿਰੀ ਚੱਕਰ ਨੂੰ ਅੱਖਾਂ ਲਈ ਸਭ ਤੋਂ ਪ੍ਰਸੰਨਤਾ ਵਜੋਂ ਮਾਨਤਾ ਦਿੱਤੀ ਹੈ. ਇਹ ਕੁਦਰਤ ਦੇ ਸਭ ਤੋਂ ਪ੍ਰੇਰਨਾਦਾਇਕ ਪੈਟਰਨਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ ਜਿਸਦਾ ਰਚਨਾਤਮਕ ਕਲਾਤਮਕ ਸਮੀਕਰਨਾਂ ਵਿੱਚ ਅਨੁਵਾਦ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।

