តារាងមាតិកា
ចាប់ពីខ្យល់ព្យុះរហូតដល់ផ្កា និងដើមស្រល់ លំនាំវង់មានច្រើននៅក្នុងធម្មជាតិ។ គណិតវិទ្យាគឺជាវិទ្យាសាស្ត្រនៃលំនាំ ដូច្នេះវាមិនគួរឱ្យភ្ញាក់ផ្អើលទេដែលវង់បានបំផុសគំនិតគណិតវិទូអស់ជាច្រើនសតវត្សមកហើយ។ វង់មួយក្នុងចំណោមវង់ទាំងនេះគឺជាវង់ពណ៌មាស ដែលគិតថាជាប្រភេទនៃកូដដែលគ្រប់គ្រងស្ថាបត្យកម្មនៃសកលលោក។ វង់ពណ៌មាសគឺជាប្រធានបទដ៏ទូលំទូលាយ និងគួរឱ្យចាប់អារម្មណ៍ ដែលបានដើរតួយ៉ាងសំខាន់ក្នុងប្រវត្តិសាស្ត្រ និងការងារសិល្បៈ។
នេះគឺជាក្រឡេកមើលវង់មាស ដែលជាប្រភពដើម អត្ថន័យ និងសារៈសំខាន់របស់វា។
តើអ្វីជានិមិត្តសញ្ញាវង់មាស?
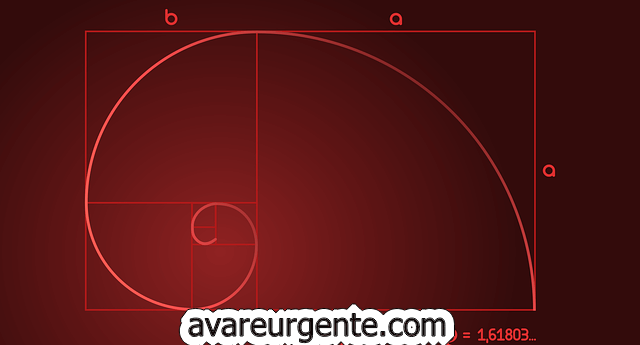
វង់មាសគឺជាលំនាំដែលត្រូវបានបង្កើតឡើងដោយផ្អែកលើគោលគំនិតនៃសមាមាត្រមាស ដែលជាច្បាប់សកលដែលតំណាងឱ្យ "ឧត្តមគតិ" នៅក្នុងគ្រប់ទម្រង់នៃជីវិត និងរូបធាតុ។ តាមពិត ជារឿយៗវាត្រូវបានលើកឡើងជាឧទាហរណ៍នៃការតភ្ជាប់រវាងច្បាប់នៃគណិតវិទ្យា និងរចនាសម្ព័ន្ធនៃភាវៈរស់។ កាលណាយើងយល់កាន់តែច្រើនអំពីគណិតវិទ្យានៅពីក្រោយនិមិត្តសញ្ញា នោះយើងនឹងពេញចិត្តចំពោះរូបរាងរបស់វានៅក្នុងធម្មជាតិ និងសិល្បៈ។
នៅក្នុងគណិតវិទ្យា សមាមាត្រមាសគឺជាលេខពិសេសដែលប្រហែលស្មើនឹង 1.618 ហើយតំណាងដោយអក្សរក្រិក។ Φ (ភី) ។ អ្នកប្រហែលជាឆ្ងល់ថាតើវង់មាសនេះមកពីណា ហើយចម្លើយចំពោះវាស្ថិតនៅក្នុងចតុកោណកែងមាស។ នៅក្នុងធរណីមាត្រ វង់មាសអាចទាញចេញពីចតុកោណកែងមាសដែលជ្រុងរបស់វាសមាមាត្រទៅតាមសមាមាត្រមាស។
នៅក្នុងឆ្នាំ 1800 គណិតវិទូជនជាតិអាឡឺម៉ង់ Martin Ohm បានហៅថាលេខពិសេស 1.618 មាស ទំនងជាព្រោះវាតែងតែមាននៅក្នុងគណិតវិទ្យា។ លើសពីនេះទៅទៀត វាត្រូវបានពិពណ៌នាថាជា ដ៏ទេវភាព ដោយសារតែភាពញឹកញាប់របស់វានៅក្នុងពិភពធម្មជាតិ។ លំនាំវង់ដែលបង្កើតចេញពីសមាមាត្រមាស ត្រូវបានគេហៅផងដែរថាវង់ មាស ។
វង់មាសធៀបនឹង Fibonacci Spiral

សមាមាត្រមាសកើតឡើងនៅក្នុងមនុស្សជាច្រើន បរិបទគណិតវិទ្យា។ នោះហើយជាមូលហេតុដែលវង់មាសត្រូវបានភ្ជាប់ជាញឹកញាប់ជាមួយលំដាប់ Fibonacci ដែលជាស៊េរីនៃលេខដែលភ្ជាប់យ៉ាងជិតស្និទ្ធជាមួយភី។ តាមបច្ចេកទេស លំដាប់ចាប់ផ្តើមដោយលេខ 0 និង 1 ហើយបន្តដោយគ្មានកំណត់ ហើយប្រសិនបើអ្នកបែងចែកលេខនីមួយៗដោយលេខមុនរបស់វា លទ្ធផលនឹងប្រែទៅជាសមាមាត្រមាស ប្រហែល 1.618។
នៅក្នុងគណិតវិទ្យា មានលំនាំវង់ជាច្រើន និង ពួកគេអាចត្រូវបានវាស់វែង។ វង់មាស និងវង់ Fibonacci មានរូបរាងស្រដៀងគ្នាខ្លាំងណាស់ ហើយមនុស្សជាច្រើនប្រើពួកវាជំនួសគ្នា ប៉ុន្តែពួកវាមិនដូចគ្នាទេ។ អ្វីគ្រប់យ៉ាងអាចត្រូវបានពន្យល់ដោយការគណនាគណិតវិទ្យា ហើយពួកវានឹងមិនមានលំនាំដូចគ្នានៅពេលវាស់។
វាត្រូវបានគេនិយាយថាវង់ Fibonacci ផ្គូផ្គងតែវង់មាសនៅចំណុចជាក់លាក់មួយ នៅពេលដែលអតីតខិតជិតសមាមាត្រមាស ឬ 1.618 ។ ជាការពិត លេខ Fibonacci កាន់តែខ្ពស់ ទំនាក់ទំនងរបស់ពួកគេកាន់តែជិតស្និទ្ធជាមួយ Phi ។ សូមចងចាំថាមិនមែនគ្រប់វង់ដែលរកឃើញក្នុងធម្មជាតិគឺផ្អែកលើលេខ Fibonacci ឬពណ៌មាសនោះទេ។ratio.
អត្ថន័យ និងនិមិត្តសញ្ញានៃវង់មាស
និមិត្តសញ្ញាវង់មាសបានបំផុសគំនិតមនុស្សរាប់មិនអស់ក្នុងប្រវត្តិសាស្ត្រ។ វាត្រូវបានផ្សារភ្ជាប់ជាមួយនឹងមូលដ្ឋានគ្រឹះនៃជីវិត ខាងវិញ្ញាណ និងការបង្កើត។
- ជីវិត និងការបង្កើត
វង់មាសមានលក្ខណៈពិសេសនៅក្នុងលក្ខណៈសម្បត្តិគណិតវិទ្យារបស់វា។ ហើយបង្ហាញថាយើងរស់នៅក្នុងសកលលោកដែលគ្រប់គ្រងដោយច្បាប់គណិតវិទ្យា។ ខណៈពេលដែលអ្នកផ្សេងទៀតជឿថាវាគ្រាន់តែជាការចៃដន្យដ៏ចម្លែកមួយ អ្នកវិទ្យាសាស្ត្រ និងអ្នកស្រាវជ្រាវជាច្រើនបានចាត់ទុកវាជាភស្តុតាងនៃគ្រូគណិតវិទូ ឬអ្នកបង្កើត។ យ៉ាងណាមិញ ការរចនាដ៏ឆ្លាតវៃនៅក្នុងធម្មជាតិគឺស្មុគស្មាញ ហើយវាហាក់ដូចជាមិនសមហេតុផលសម្រាប់អ្នកដែលគិតថាវាកើតឡើងដោយចៃដន្យ។
- តុល្យភាព និងភាពសុខដុមរមនា
វង់មាសបានចាប់យកការស្រមើលស្រមៃរបស់គណិតវិទូ អ្នករចនា និងវិចិត្រករ ជាមួយនឹងភាពស្រស់ស្អាតរបស់វា។ វាត្រូវបានឆ្លុះបញ្ចាំងនៅក្នុងស្នាដៃដ៏អស្ចារ្យបំផុតមួយចំនួននៃសិល្បៈ និងស្ថាបត្យកម្ម។ វាក៏ត្រូវបានផ្សារភ្ជាប់ជាមួយនឹងភាពស្រស់ស្អាតផងដែរ ដោយសារតែមនុស្សជាច្រើនជឿថាភាពស្រស់ស្អាតគឺផ្តោតលើលក្ខណៈសម្បត្តិតែមួយគត់របស់វានៅក្នុងគណិតវិទ្យា និងធរណីមាត្រ។ អាថ៌កំបាំងខ្លះជឿថានិមិត្តសញ្ញានេះក៏នឹងនាំមកនូវតុល្យភាព និងភាពសុខដុមរមនាក្នុងជីវិតរបស់មនុស្សផងដែរ។
និមិត្តសញ្ញាវង់មាសក្នុងប្រវត្តិសាស្ត្រ
ភាពទាក់ទាញជាមួយនឹងនិមិត្តសញ្ញាវង់មាសបាននាំឱ្យសិល្បករជាច្រើនប្រើវានៅក្នុងរបស់ពួកគេ ស្នាដៃ។ មានឱកាសល្អដែលអ្នកបានឃើញរួចហើយនូវនិមិត្តសញ្ញាជាផ្ទាំងគំនូរលើសិល្បៈផ្សេងៗទម្រង់ពី Parthenon ទៅ Mona Lisa ។ ជាអកុសល មានការអះអាងច្រលំជាច្រើនអំពីប្រធានបទ ដូច្នេះយើងនឹងជួយអ្នកក្នុងការសម្រេចចិត្តថាតើពួកគេមានមូលដ្ឋាននៅក្នុងទេវកថា ឬគណិតវិទ្យា។
- The Parthenon

ត្រូវបានសាងសង់ឡើងនៅចន្លោះឆ្នាំ 447 និង 438 មុនគ.ស. វិមាន Parthenon នៅទីក្រុងអាថែន ប្រទេសក្រិច គឺជាសំណង់ដ៏មានសោភ័ណភាពបំផុតមួយដែលមិនធ្លាប់មាន។ មនុស្សជាច្រើនប៉ាន់ស្មានថាវាត្រូវបានសាងសង់ដោយផ្អែកលើសមាមាត្រមាស។ អ្នកថែមទាំងនឹងឃើញរូបភាពជាច្រើននៃផ្នែកខាងមុខនៃប្រាសាទជាមួយនឹងវង់ពណ៌មាស និងចតុកោណកែងមាសនៅលើវា។
គ្មានអ្វីគួរឱ្យសង្ស័យទេដែលថាជនជាតិក្រិចបុរាណបានបញ្ចូលគណិតវិទ្យា និងធរណីមាត្រទៅក្នុងស្ថាបត្យកម្មរបស់ពួកគេ ប៉ុន្តែអ្នកប្រាជ្ញមិនអាច ស្វែងរកភស្តុតាងជាក់ស្តែងដែលថាពួកគេបានប្រើសមាមាត្រមាសក្នុងការសាងសង់ Parthenon ។ មនុស្សជាច្រើនយល់ឃើញថាវាជាទេវកថា ពីព្រោះទ្រឹស្តីបទគណិតវិទ្យាភាគច្រើនត្រូវបានបង្កើតឡើងតែបន្ទាប់ពីការសាងសង់ប្រាសាទ។
លើសពីនេះទៅទៀត ការវាស់វែងច្បាស់លាស់គឺត្រូវការជាចាំបាច់ ដើម្បីសន្និដ្ឋានថាសមាមាត្រមាស និងវង់មាសត្រូវបានប្រើប្រាស់នៅក្នុង ការរចនា។ យោងតាមអ្នកជំនាញ ចតុកោណកែងមាសគួរតែត្រូវបានដាក់នៅមូលដ្ឋាននៃជំហានឆ្ពោះទៅរក Parthenon មិនមែននៅមូលដ្ឋាននៃជួរឈររបស់វានោះទេ—ដូចដែលបានបង្ហាញជាទូទៅនៅក្នុងរូបភាពមួយចំនួន។ ផងដែរ រចនាសម្ព័ននេះស្ថិតក្នុងការបំផ្លិចបំផ្លាញ ដែលធ្វើឲ្យវិមាត្រពិតប្រាកដរបស់វាអាស្រ័យទៅតាមការប៉ាន់ស្មានមួយចំនួន។
- រូបគំនូររបស់ Leonardo da Vinci

Leonardo ដាវីនស៊ី ត្រូវបានគេដាក់ឈ្មោះថា "ទេវភាព" ជាយូរមកហើយវិចិត្រករភ្ជាប់ជាមួយសមាមាត្រមាស។ សមាគមនេះថែមទាំងត្រូវបានគាំទ្រដោយប្រលោមលោក The Da Vinci Code ដោយសារតែគ្រោងនេះពាក់ព័ន្ធនឹងសមាមាត្រមាស និងលេខ Fibonacci ។ ខណៈពេលដែលអ្វីៗទាំងអស់ត្រូវមានការបកស្រាយ មនុស្សជាច្រើនបានសន្និដ្ឋានថាវិចិត្រករបានប្រើវង់ពណ៌មាសក្នុងស្នាដៃរបស់គាត់ដោយចេតនាដើម្បីសម្រេចបាននូវតុល្យភាព និងភាពស្រស់ស្អាត។
ការប្រើប្រាស់សមាមាត្រមាសរបស់ Da Vinci គឺជាក់ស្តែងនៅក្នុង អាហារចុងក្រោយ និង The Annuciation ប៉ុន្តែ Mona Lisa ឬ La Joconde នៅតែត្រូវបានពិភាក្សានៅឡើយ។ វាត្រូវបានគេនិយាយថាមានធាតុស្ថាបត្យកម្មតិចតួចនិងបន្ទាត់ត្រង់ដែលត្រូវប្រើជាចំណុចយោងបើប្រៀបធៀបទៅនឹងគំនូរពីរផ្សេងទៀត។ ទោះយ៉ាងណាក៏ដោយ អ្នកអាចរកឃើញការបកស្រាយជាច្រើននៃសមាមាត្រមាសនៅលើ Mona Lisa ដែលមានវង់ពណ៌មាសជាការលាបលើ។
យើងប្រហែលជាមិនដែលដឹងពីចេតនារបស់ Da Vinci សម្រាប់ស្នាដៃរបស់គាត់ទេ ប៉ុន្តែមនុស្សជាច្រើនបានរកឃើញការចៃដន្យដ៏គួរឱ្យទាក់ទាញ។ ដោយសារការប្រើប្រាស់ពីមុនរបស់វិចិត្រករ វាមិននឹកស្មានដល់សម្រាប់គាត់ក្នុងការប្រើវានៅលើគំនូរនោះផងដែរ។ សូមចងចាំថា មិនមែនគ្រប់គំនូររបស់ Da Vinci មានភស្តុតាងច្បាស់លាស់នៃការបញ្ចូលសមាមាត្រមាស និងវង់មាសនោះទេ ដូច្នេះហើយ វាជាការលំបាកក្នុងការសន្និដ្ឋានថាស្នាដៃរបស់គាត់ទាំងអស់គឺផ្អែកលើពួកវា។
និមិត្តសញ្ញាវង់មាសនៅក្នុង សម័យទំនើប
វង់មាសរួមចំណែកដល់ការយល់ដឹងរបស់យើងអំពីជីវិត និងសកលលោក។ នេះគឺជារបកគំហើញថ្មីៗមួយចំនួនទាក់ទងនឹងនិមិត្តសញ្ញា៖
- នៅក្នុងគណិតវិទ្យា
វង់មាសដើរតួនាទីក្នុងធរណីមាត្រនៃប្រភាគ ដែលជាលំនាំស្មុគស្មាញដែលធ្វើម្តងទៀតជារៀងរហូត។ គណិតវិទូជនជាតិអាមេរិក Edmund Harriss បានក្លាយជាមនុស្សពេញនិយមសម្រាប់ខ្សែកោង fractal របស់គាត់ដោយផ្អែកលើវង់មាស ដែលឥឡូវនេះត្រូវបានគេស្គាល់ថាជា Harriss Spiral ។ វាត្រូវបានគេនិយាយថាគាត់មានបំណងគូរវង់មែកដែលមើលទៅគួរឱ្យទាក់ទាញ ប៉ុន្តែគាត់បានបញ្ចប់ដោយវង់តែមួយដោយប្រើដំណើរការគណិតវិទ្យា។
- នៅក្នុងជីវមេកានិច
វង់ពណ៌មាសត្រូវបានគេគិតថាមានឥទ្ធិពលគួរឱ្យចាប់អារម្មណ៍លើចលនានៃដៃមនុស្ស។ យោងតាមអ្នកជំនាញកាយវិភាគវិទ្យា ចលនានៃម្រាមដៃរបស់មនុស្សដើរតាមលំនាំនៃវង់មាស។ អ្នកនឹងឃើញរូបភាពនៃកណ្តាប់ដៃដែលមានសញ្ញាវង់ជាការលាបលើ។
- ក្នុងការរចនា និងសមាសភាព
បច្ចុប្បន្ន អ្នករចនាជាច្រើនបានដាក់ជាន់លើ។ និមិត្តសញ្ញាវង់មាសនៅលើរូបភាព ដើម្បីបង្ហាញពីសមាមាត្រសមាមាត្រមាសរបស់វា ក្នុងក្តីសង្ឃឹមនៃការសម្រេចបាននូវភាពសុខដុមរមនាដែលមើលឃើញនៅក្នុងស្នាដៃរបស់ពួកគេ។ រូបសញ្ញា និងរូបសញ្ញាទំនើបមួយចំនួនគឺផ្អែកលើពួកវា ដែលអ្នករចនាអនុវត្តនូវគំនិតដែលគេហៅថា "សមាមាត្រក្នុងសមាមាត្រ។"
- នៅក្នុងធម្មជាតិ
ធម្មជាតិពោរពេញដោយលំនាំវង់ ប៉ុន្តែការស្វែងរកវង់ពណ៌មាសពិតប្រាកដនៅក្នុងធម្មជាតិគឺកម្រណាស់។ គួរឱ្យចាប់អារម្មណ៍ អ្នកវិទ្យាសាស្ត្របានរកឃើញថា សត្វក្ងោកហើរក្នុងផ្លូវវង់ពណ៌មាស នៅពេលចូលទៅជិតសត្វរបស់វា ទំនងដោយសារតែវាជាផ្លូវហោះហើរដែលសន្សំសំចៃថាមពល។
ផ្ទុយពីជំនឿដ៏ពេញនិយម សែល nautilus មិនមែនជាវង់មាសទេ។ នៅពេលវាស់វែង ទាំងពីរនឹងមិនផ្គូផ្គងគ្នាទេ ទោះបីជាពួកគេត្រូវបានតម្រឹម ឬមាត្រដ្ឋានយ៉ាងណាក៏ដោយ។ ម្យ៉ាងវិញទៀត មិនមែនគ្រប់សម្បក nautilus ត្រូវបានបង្កើតឡើងស្មើៗគ្នានោះទេ ដោយសារនីមួយៗមានការប្រែប្រួល និងភាពមិនល្អឥតខ្ចោះនៃរាង។
វង់នៃផ្កាឈូករ័ត្ន និងដើមស្រល់គឺស្អាត ប៉ុន្តែពួកវាមិនមែនជាវង់ពណ៌មាសទេ។ តាមពិត វង់របស់ពួកគេមិនរុំជុំវិញកណ្តាលទេ ផ្ទុយពីវង់មាស។ ខណៈពេលដែលផ្កាខ្លះមានផ្កាមួយចំនួនដែលត្រូវនឹងលេខ Fibonacci មានករណីលើកលែងជាច្រើនដែលបានរកឃើញ។
អ្នកជំនាញក៏និយាយផងដែរថា កាឡាក់ស៊ី ឬពពកព្យុះម្តងម្កាលដែលសមនឹងផ្នែកនៃវង់មាស មិនគួរជាការសន្និដ្ឋាននោះទេ។ ថាកាឡាក់ស៊ី និងព្យុះសង្ឃរាទាំងអស់គឺផ្អែកលើសមាមាត្រមាស។
ដោយសង្ខេប
សកលលោករបស់យើងពោរពេញទៅដោយវង់ ដូច្នេះវាមិនគួរឱ្យភ្ញាក់ផ្អើលទេដែលមនុស្សជាច្រើនចាប់អារម្មណ៍នឹងគណិតវិទ្យានៅពីក្រោយពួកវា និងអត្ថន័យរបស់វា។ . វិចិត្រករបានទទួលស្គាល់វង់មាសជាយូរមកហើយថាជាទីគាប់ភ្នែកបំផុត។ វាពិតជាគំរូមួយក្នុងចំណោមគំរូដែលបំផុសគំនិតបំផុតនៅក្នុងធម្មជាតិ ដែលអាចបកប្រែទៅជាការបង្ហាញសិល្បៈប្រកបដោយភាពច្នៃប្រឌិត។

