Taula de continguts
Des d'huracans fins a flors i pinyes, els patrons en espiral són abundants a la natura. Les matemàtiques són la ciència dels patrons, així que no és estrany que les espirals hagin inspirat els matemàtics durant segles. Una d'aquestes espirals és l'espiral daurada, pensada com una mena de codi que regeix l'arquitectura de l'univers. L'espiral daurada és un tema ampli i fascinant que ha tingut un paper destacat en la història i les obres d'art.
A continuació, es mostra l'espiral daurada: el seu origen, significats i significat.
Què és el símbol de l'espiral daurada?
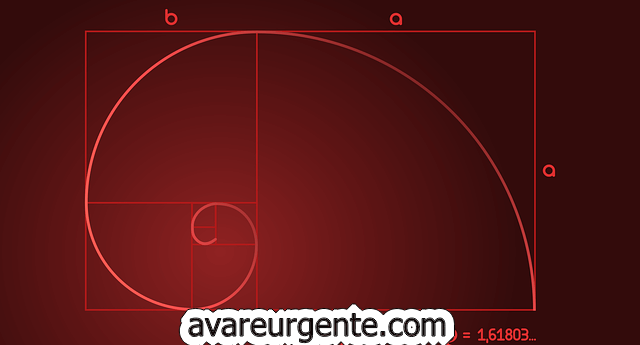
L'espiral daurada és un patró creat a partir del concepte de proporció àuria, una llei universal que representa l'"ideal" en totes les formes de vida i matèria. De fet, sovint es cita com a exemple de la connexió entre les lleis de les matemàtiques i l'estructura dels éssers vius. Com més entenem les matemàtiques darrere del símbol, més apreciarem les seves aparicions a la natura i les arts.
En matemàtiques, la proporció àuria és un nombre especial que és aproximadament igual a 1,618 i representat per la lletra grega. Φ (Fi). Podeu preguntar-vos d'on ve aquesta espiral daurada, i la resposta a això es troba dins del rectangle daurat. En geometria, l'espiral daurada es pot dibuixar a partir d'un rectangle daurat els costats del qual estan proporcionats segons la proporció àuria.
A l'any 1800, el matemàtic alemany Martin Ohm va anomenar elnúmero especial 1.618 daurat , probablement perquè sempre ha existit en matemàtiques. Més enrere en el temps, fins i tot es va descriure com a diví per la seva freqüència en el món natural. El patró d'espiral creat a partir de la proporció àuria també s'anomena espiral daurada .
L'espiral daurada enfront de l'espiral de Fibonacci

La proporció àuria es produeix en molts contextos matemàtics. És per això que l'espiral daurada s'associa sovint amb la seqüència de Fibonacci, una sèrie de nombres estretament vinculats a Phi. Tècnicament, la seqüència comença per 0 i 1 i continua infinitament, i si es divideix cada nombre pel seu predecessor, el resultat convergiria a la proporció àuria, aproximadament 1,618.
En matemàtiques, hi ha diversos patrons en espiral i es poden mesurar. L'espiral daurada i l'espiral de Fibonacci tenen una forma molt semblant, i molts les utilitzen indistintament, però no són el mateix. Tot es pot explicar amb càlculs matemàtics, i no tindran el mateix patró exacte quan es mesuren.
Es diu que l'espiral de Fibonacci només coincideix amb l'espiral daurada en un punt determinat, quan la primera s'acosta a la proporció àuria. o 1.618. De fet, com més alts són els nombres de Fibonacci, més propera és la seva relació amb Phi. Només cal tenir en compte que no totes les espirals que es troben a la natura es basen en els nombres de Fibonacci o els dauratsratio.
Significat i simbolisme de l'espiral daurada
El símbol de l'espiral daurada ha inspirat innombrables persones al llarg de la història. S'ha associat amb els fonaments de la vida, l'espiritualitat i la creació.
- Vida i creació
L'espiral daurada és única en les seves propietats matemàtiques. i demostra que vivim en un univers regit per lleis matemàtiques. Mentre que altres creuen que és només una coincidència molt estranya, molts científics i investigadors ho consideren una evidència d'un mestre matemàtic o un creador. Al cap i a la fi, el disseny intel·ligent a la natura és complex, i a alguns pot semblar il·lògic pensar que va sorgir per casualitat.
- Equilibri i harmonia
L'espiral daurada ha captat la imaginació de matemàtics, dissenyadors i artistes amb la seva bellesa. Es reflecteix en algunes de les millors obres d'art i arquitectura. També s'ha associat amb la bellesa, ja que molts creuen que la bellesa es centra en les seves propietats úniques en matemàtiques i geometria. Alguns místics creuen que el símbol també aportarà equilibri i harmonia a la vida d'un.
El símbol de l'espiral daurada a la història
La fascinació pel símbol de l'espiral daurada ha portat a molts artistes a utilitzar-lo en les seves obres mestres. Hi ha moltes possibilitats que ja hagis vist el símbol com a superposicions en diferents artsformes, des del Partenó fins a la Mona Lisa. Malauradament, hi ha moltes afirmacions confuses sobre el tema, així que t'ajudarem a decidir si es basen en mites o matemàtiques.
- El Partenó

Construït entre el 447 i el 438 aC, el Partenó d'Atenes, Grècia, és una de les estructures més agradables estèticament mai fetes. Molts especulen que es va construir a partir de la proporció àuria. Fins i tot veureu diverses representacions de la façana frontal del temple amb l'espiral daurada i el rectangle daurat.
No hi ha dubte que els antics grecs van incorporar les matemàtiques i la geometria a la seva arquitectura, però els estudiosos no poden. trobar proves concretes que van utilitzar la proporció àuria per construir el Partenó. Molts ho troben com un mite perquè la majoria dels teoremes matemàtics només es van desenvolupar després de la construcció del temple.
A més, calen mesures precises per concloure que la proporció àuria i l'espiral dauria es van utilitzar en el disseny. Segons els experts, el rectangle daurat s'hauria d'emmarcar a la base dels graons que s'acosten al Partenó, no a la base de les seves columnes, com es mostra habitualment en diverses il·lustracions. A més, l'estructura està en ruïnes, la qual cosa fa que les seves dimensions exactes estiguin subjectes a alguna estimació.
- Pintures de Leonardo da Vinci

Leonardo Da Vinci ha estat batejat durant molt de temps el "diví"pintor associat a la proporció àuria. Aquesta associació fins i tot va ser recolzada per la novel·la El codi Da Vinci , ja que la trama inclou la proporció àuria i els nombres de Fibonacci. Tot i que tot està subjecte a interpretació, molts han especulat que el pintor va utilitzar intencionadament l'espiral daurada en les seves obres per aconseguir l'equilibri i la bellesa.
L'ús de Da Vinci de la proporció àuria és evident a L'últim sopar i La Anunciació , però la Mona Lisa o La Joconde encara es debat. Es diu que hi ha pocs elements arquitectònics i línies rectes per utilitzar com a punts de referència en comparació amb les altres dues pintures. Tot i així, podeu trobar diverses interpretacions de les proporcions àuries a la Mona Lisa, amb l'espiral daurada com a superposicions.
Probablement mai sabrem la intenció de Da Vinci amb les seves obres mestres, però a molts consideren convincent aquesta estranya coincidència. Tenint en compte l'ús previ del pintor, no seria inesperat que també l'utilitzi a l'esmentat quadre. Només cal tenir en compte que no tots els quadres de Da Vinci tenen evidències clares de la incorporació de la proporció àuria i l'espiral daurada, per la qual cosa és difícil concloure que totes les seves obres mestres es basen en elles.
El símbol de l'espiral daurada a Temps moderns
L'espiral daurada contribueix a la nostra comprensió de la vida i de l'univers. Aquests són alguns dels descobriments recents sobre elsímbol:
- En matemàtiques
L'espiral daurada juga un paper en la geometria dels fractals, un patró complex que es repeteix per sempre. El matemàtic nord-americà Edmund Harriss es va fer popular per la seva corba fractal basada en l'espiral daurada, ara coneguda com l'espiral de Harriss. Es diu que pretenia dibuixar espirals ramificades que semblen estèticament atractives, però va acabar amb una espiral única mitjançant un procés matemàtic.
- En biomecànica
Es creu que l'espiral daurada té una influència fascinant sobre el moviment de la mà humana. Segons un anatomista, el moviment dels dits humans segueix el patró de l'espiral daurada. Fins i tot trobareu imatges d'un puny tancat amb el símbol de l'espiral com a superposició.
- A Disseny i composició
Avui en dia, molts dissenyadors se superposen. un símbol d'espiral daurat en una imatge per il·lustrar les seves proporcions de proporció àuria amb l'esperança d'aconseguir l'harmonia visual en les seves obres. Alguns logotips i icones moderns es basen en ells, on els dissenyadors apliquen l'anomenat concepte de "ràtios dins de proporcions".
- A la natura
La natura està plena de patrons en espiral, però trobar l'espiral daurada real a la natura és rar. Curiosament, els científics han descobert que els falcons volen en una espiral daurada quan s'apropen a la seva presa, probablement perquè és una ruta de vol eficient energèticament.
Contràriament al que passa.creença popular, la closca del nautilus no és una espiral daurada. Quan es mesuren, els dos no coincidirien sense importar com estiguessin alineats o escalats. A més, no totes les closques de nàutils són iguals, ja que cadascuna té variacions i imperfeccions en les formes.
Les espirals de gira-sols i pinyes són boniques, però no són espirals daurades. De fet, les seves espirals ni tan sols s'emboliquen al centre, a diferència de l'espiral daurada. Tot i que algunes flors tenen un nombre de pètals que es corresponen amb els nombres de Fibonacci, s'han trobat diverses excepcions.
Els experts també diuen que una galàxia o núvol de tempesta ocasional que s'ajusti a una part d'una espiral daurada no hauria de ser una conclusió. que totes les galàxies i huracans es basen en la proporció àuria.
En breu
El nostre univers està ple d'espirals, així que no és d'estranyar que molts s'hagin interessat per les matemàtiques que hi ha darrere i els seus significats. . Els artistes han reconegut des de fa temps que l'espiral daurada és la més agradable als ulls. De fet, és un dels patrons més inspiradors de la natura que es pot traduir en expressions artístiques creatives.

