سمندری طوفان سے لے کر پھولوں اور پائنکونز تک، سرپل پیٹرن فطرت میں بکثرت ہیں۔ ریاضی پیٹرن کی سائنس ہے، لہذا یہ حیرت کی بات نہیں ہے کہ سرپل نے صدیوں سے ریاضی دانوں کو متاثر کیا ہے۔ ان سرپلوں میں سے ایک سنہری سرپل ہے، جسے ایک قسم کا کوڈ سمجھا جاتا ہے جو کائنات کے فن تعمیر کو کنٹرول کرتا ہے۔ گولڈن سرپل ایک وسیع، دلچسپ موضوع ہے جس نے تاریخ اور فن کے کاموں میں نمایاں کردار ادا کیا ہے۔

یہاں سنہری سرپل پر ایک نظر ہے – اس کی اصل، معنی اور اہمیت۔

گولڈن اسپائرل کی علامت کیا ہے؟

سنہری سرپل ایک ایسا نمونہ ہے جو سنہری تناسب کے تصور کی بنیاد پر بنایا گیا ہے—ایک عالمگیر قانون جو زندگی اور مادے کی تمام شکلوں میں "مثالی" کی نمائندگی کرتا ہے۔ درحقیقت، اسے اکثر ریاضی کے قوانین اور جانداروں کی ساخت کے درمیان تعلق کی مثال کے طور پر پیش کیا جاتا ہے۔ جتنا زیادہ ہم علامت کے پیچھے کی ریاضی کو سمجھیں گے، اتنا ہی ہم فطرت اور فنون میں اس کی ظاہری شکل کی تعریف کریں گے۔

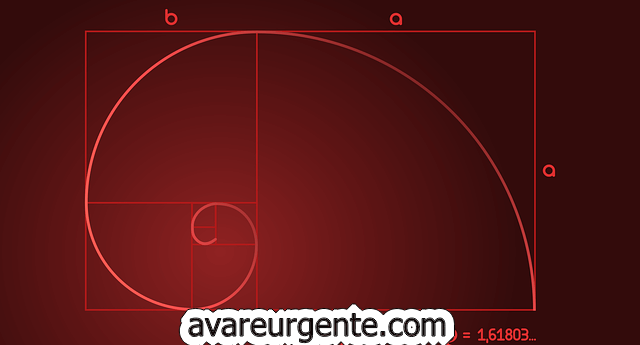
ریاضی میں، سنہری تناسب ایک خاص عدد ہے جو تقریباً 1.618 کے برابر ہے اور یونانی خط سے ظاہر ہوتا ہے۔ Φ (Phi)۔ آپ حیران ہوں گے کہ یہ سنہری سرپل کہاں سے آیا ہے اور اس کا جواب سنہری مستطیل میں ہے۔ جیومیٹری میں، سنہری سرپل کو ایک سنہری مستطیل سے کھینچا جا سکتا ہے جس کے اطراف سنہری تناسب کے مطابق ہوتے ہیں۔

1800 کی دہائی میں جرمن ریاضی دان مارٹن اوہم نےخاص نمبر 1.618 سنہری ، اس لیے کہ یہ ہمیشہ سے ریاضی میں موجود ہے۔ وقت کے ساتھ ساتھ، قدرتی دنیا میں اس کی تعدد کی وجہ سے اسے خدائی کے طور پر بھی بیان کیا گیا تھا۔ سنہری تناسب سے بنائے گئے سرپل پیٹرن کو سنہری سرپل بھی کہا جاتا ہے۔

گولڈن اسپائرل بمقابلہ فبونیکی اسپائرل

سنہری تناسب بہت سے حصوں میں پایا جاتا ہے۔ ریاضیاتی سیاق و سباق یہی وجہ ہے کہ سنہری سرپل اکثر فبونیکی ترتیب کے ساتھ منسلک ہوتا ہے - نمبروں کا ایک سلسلہ جو Phi سے قریب سے جڑا ہوا ہے۔ تکنیکی طور پر، ترتیب 0 اور 1 سے شروع ہوتی ہے اور لامحدود طور پر جاری رہتی ہے، اور اگر آپ ہر نمبر کو اس کے پیشرو سے تقسیم کرتے ہیں، تو نتیجہ سنہری تناسب میں بدل جائے گا، تقریباً 1.618۔

ریاضی میں، کئی سرپل پیٹرن ہوتے ہیں اور وہ ماپا جا سکتا ہے. سنہری سرپل اور فبونیکی سرپل شکل میں بہت ملتے جلتے ہیں، اور بہت سے لوگ ان کو ایک دوسرے کے بدلے استعمال کرتے ہیں، لیکن وہ ایک جیسے نہیں ہیں۔ ہر چیز کی ریاضی کے حساب سے وضاحت کی جا سکتی ہے، اور ناپتے وقت ان کا صحیح نمونہ نہیں ہوگا۔

کہا جاتا ہے کہ فبونیکی سرپل صرف ایک خاص نقطہ پر سنہری سرپل سے میل کھاتا ہے، جب سابقہ ​​سنہری تناسب کے قریب آتا ہے۔ یا 1.618۔ درحقیقت، فبونیکی نمبرز جتنے زیادہ ہوں گے، ان کا تعلق Phi سے اتنا ہی قریبی ہے۔ بس ذہن میں رکھیں کہ فطرت میں پایا جانے والا ہر سرپل فبونیکی نمبر یا سنہری پر مبنی نہیں ہے۔تناسب۔

سنہری سرپل کے معنی اور علامت

سنہری سرپل کی علامت نے پوری تاریخ میں لاتعداد لوگوں کو متاثر کیا ہے۔ اس کا تعلق زندگی، روحانیت اور تخلیق کے بنیادی اصولوں سے ہے۔

• زندگی اور تخلیق

سنہری سرپل اپنی ریاضیاتی خصوصیات میں منفرد ہے۔ اور ثابت کرتا ہے کہ ہم ایک ایسی کائنات میں رہتے ہیں جو ریاضی کے قوانین کے تحت چلتی ہے۔ جب کہ دوسروں کا خیال ہے کہ یہ صرف ایک بہت ہی عجیب اتفاق ہے، بہت سے سائنس دان اور محققین اسے ایک ماہر ریاضی دان یا تخلیق کار کا ثبوت سمجھتے ہیں۔ بہر حال، فطرت میں ذہین ڈیزائن پیچیدہ ہے، اور کچھ لوگوں کے لیے یہ سوچنا غیر منطقی لگ سکتا ہے کہ یہ اتفاقاً ہوا ہے۔

• توازن اور ہم آہنگی

تاریخ میں سنہری سرپل علامت

سنہری سرپل علامت کے ساتھ دلچسپی نے بہت سے فنکاروں کو اسے اپنی زندگی میں استعمال کرنے پر مجبور کیا ہے۔ شاہکار اس بات کا ایک اچھا موقع ہے کہ آپ نے علامت کو پہلے ہی مختلف آرٹ پر اوورلیز کے طور پر دیکھا ہے۔شکلیں، پارتھینن سے مونا لیزا تک۔ بدقسمتی سے، اس موضوع کے بارے میں بہت سے الجھے ہوئے دعوے ہیں، اس لیے ہم آپ کو یہ فیصلہ کرنے میں مدد کریں گے کہ آیا وہ افسانہ یا ریاضی پر مبنی ہیں۔

• The Parthenon

اس میں کوئی شک نہیں کہ قدیم یونانیوں نے ریاضی اور جیومیٹری کو اپنے فن تعمیر میں شامل کیا تھا، لیکن علماء ایسا نہیں کر سکتے۔ ٹھوس شواہد تلاش کریں کہ انہوں نے پارتھینن کی تعمیر میں سنہری تناسب کا استعمال کیا۔ بہت سے لوگ اسے ایک افسانہ سمجھتے ہیں کیونکہ زیادہ تر ریاضیاتی تھیورمز مندر کی تعمیر کے بعد ہی تیار کیے گئے تھے۔

مزید یہ ہے کہ یہ نتیجہ اخذ کرنے کے لیے درست پیمائش کی ضرورت ہے کہ سنہری تناسب اور سنہری سرپل استعمال کیا گیا تھا۔ ڈیزائن ماہرین کے مطابق، سنہری مستطیل کو پارتھینن کے قریب آنے والے قدموں کی بنیاد پر بنایا جانا چاہیے، نہ کہ اس کے کالموں کی بنیاد پر، جیسا کہ عام طور پر کئی مثالوں میں دکھایا گیا ہے۔ اس کے علاوہ، ڈھانچہ کھنڈرات میں ہے، جس کی وجہ سے اس کے درست طول و عرض کو کسی اندازے سے مشروط کیا جاتا ہے۔

• لیونارڈو ڈاونچی کی پینٹنگز

لیونارڈو ڈاونچی کو طویل عرصے سے "الہی" کہا جاتا رہا ہے۔سنہری تناسب کے ساتھ منسلک پینٹر. یہاں تک کہ اس ایسوسی ایشن کو ناول دا ونچی کوڈ نے بھی سپورٹ کیا، کیونکہ پلاٹ میں سنہری تناسب اور فبونیکی نمبر شامل ہیں۔ اگرچہ ہر چیز تشریح کے تابع ہے، بہت سے لوگوں نے قیاس کیا ہے کہ مصور نے جان بوجھ کر سنہری سرپل کو توازن اور خوبصورتی حاصل کرنے کے لیے اپنے کاموں میں استعمال کیا۔

ڈاونچی کا سنہری تناسب کا استعمال دی لاسٹ سپر اور The Annuciation ، لیکن مونا لیزا یا La Joconde ابھی بھی بحث کے لیے ہے۔ کہا جاتا ہے کہ دیگر دو پینٹنگز کے مقابلے میں کچھ آرکیٹیکچرل عناصر اور سیدھی لکیریں حوالہ پوائنٹ کے طور پر استعمال کی جا سکتی ہیں۔ پھر بھی، آپ مونا لیزا پر سنہری تناسب کی کئی تشریحات تلاش کر سکتے ہیں، جس میں سنہری سرپل کو اوورلیز کے طور پر نمایاں کیا گیا ہے۔

ہمیں شاید کبھی بھی ڈاونچی کے شاہکاروں کے لیے ان کے ارادے کا علم نہیں ہوگا، لیکن بہت سے لوگوں کو عجیب اتفاق زبردست لگتا ہے۔ پینٹر کے پیشگی استعمال کو دیکھتے ہوئے، اس کے لیے مذکورہ پینٹنگ پر بھی استعمال کرنا غیر متوقع نہیں ہوگا۔ بس ذہن میں رکھیں کہ ہر ڈاونچی کی پینٹنگ میں سنہری تناسب اور سنہری سرپل کے شامل ہونے کا واضح ثبوت نہیں ہے، اس لیے یہ نتیجہ اخذ کرنا مشکل ہے کہ اس کے تمام شاہکار ان پر مبنی ہیں۔

گولڈن اسپائرل کی علامت ماڈرن ٹائمز

سنہری سرپل زندگی اور کائنات کے بارے میں ہماری سمجھ میں معاون ہے۔ کے حوالے سے حالیہ دریافتوں میں سے کچھ یہ ہیں۔علامت:

• ریاضی میں

سنہری سرپل فریکٹلز کی جیومیٹری میں ایک کردار ادا کرتا ہے، ایک پیچیدہ نمونہ جو ہمیشہ کے لیے دہرایا جاتا ہے۔ امریکی ریاضی دان ایڈمنڈ ہیرس سنہری سرپل پر مبنی اپنے فریکٹل کریو کے لیے مشہور ہوئے، جسے اب ہیرس اسپائرل کہا جاتا ہے۔ کہا جاتا ہے کہ اس کا مقصد برانچنگ اسپرل کھینچنا تھا جو کہ جمالیاتی طور پر دلکش نظر آتے ہیں، لیکن اس نے ریاضی کے عمل کا استعمال کرتے ہوئے ایک منفرد سرپل حاصل کیا۔

• بائیو مکینکس میں
<1 یہ خیال کیا جاتا ہے کہ سنہری سرپل انسانی ہاتھ کی حرکت پر ایک دلچسپ اثر رکھتی ہے۔ ایک اناٹومسٹ کے مطابق انسانی انگلیوں کی حرکت سنہری سرپل کی طرز پر چلتی ہے۔ یہاں تک کہ آپ کو سرپل کی علامت کے ساتھ چپکی ہوئی مٹھی کی تصاویر بھی اوورلے کے طور پر ملیں گی۔
• ڈیزائن اور کمپوزیشن میں

آج کل، بہت سے ڈیزائنرز اوورلے کرتے ہیں ان کے کاموں میں بصری ہم آہنگی حاصل کرنے کی امید میں اس کے سنہری تناسب کے تناسب کو واضح کرنے کے لیے تصویر پر ایک سنہری سرپل علامت۔ کچھ جدید لوگو اور شبیہیں ان پر مبنی ہیں، جہاں ڈیزائنرز "تناسب کے اندر تناسب" کے نام نہاد تصور کا اطلاق کرتے ہیں۔

• فطرت میں

فطرت سرپل کے نمونوں سے بھری ہوئی ہے لیکن فطرت میں حقیقی سنہری سرپل تلاش کرنا نایاب ہے۔ دلچسپ بات یہ ہے کہ سائنس دانوں کو پتہ چلا ہے کہ فالکن اپنے شکار کے قریب پہنچنے پر سنہری سرپل والے راستے میں اڑتے ہیں، اس لیے کہ یہ توانائی کی بچت کا راستہ ہے۔

اس کے برعکسمقبول عقیدہ، نوٹلس شیل ایک سنہری سرپل نہیں ہے. جب ماپا جاتا ہے، تو دونوں مماثل نہیں ہوں گے چاہے وہ کس طرح منسلک ہوں یا پیمانہ ہوں۔ نیز، ہر نوٹیلس شیل کو برابر نہیں بنایا جاتا، کیونکہ ہر ایک کی شکلوں میں تغیرات اور خامیاں ہوتی ہیں۔

سورج مکھی اور پائنکونز کے سرپل خوبصورت ہوتے ہیں، لیکن وہ سنہری سرپل نہیں ہوتے ہیں۔ درحقیقت، سنہری سرپل کے برعکس، ان کے سرپل مرکز کے گرد بھی نہیں لپیٹتے ہیں۔ جب کہ کچھ پھولوں میں پنکھڑیوں کی تعداد ہوتی ہے جو فبونیکی نمبروں سے مطابقت رکھتی ہے، اس میں کئی مستثنیات پائے جاتے ہیں۔

ماہرین یہ بھی کہتے ہیں کہ کہکشاں یا کبھی کبھار طوفانی بادل جو سنہری سرپل کے حصے میں فٹ بیٹھتے ہیں، کوئی نتیجہ نہیں نکلنا چاہیے۔ کہ تمام کہکشائیں اور سمندری طوفان سنہری تناسب پر مبنی ہیں۔

بھی دیکھو: عاشورا کیا ہے؟ اسلامی مقدس دن کے حقائق اور تاریخ

مختصر میں

ہماری کائنات سرپلوں سے بھری ہوئی ہے، اس لیے یہ حیرت کی بات نہیں ہے کہ بہت سے لوگوں کو ان کے پیچھے کی ریاضی اور ان کے معنی میں دلچسپی ہو گئی ہے۔ . فنکاروں نے طویل عرصے سے سنہری سرپل کو آنکھوں کے لیے سب سے زیادہ خوش کن تسلیم کیا ہے۔ یہ واقعی فطرت کے سب سے متاثر کن نمونوں میں سے ایک ہے جس کا ترجمہ تخلیقی فنکارانہ اظہار میں کیا جا سکتا ہے۔