सामग्री तालिका
तुफानदेखि फूल र पाइनकोनसम्म, सर्पिल ढाँचाहरू प्रकृतिमा प्रशस्त छन्। गणित ढाँचाको विज्ञान हो, त्यसैले यो अचम्मको कुरा होइन कि सर्पिलहरूले गणितज्ञहरूलाई शताब्दीयौंदेखि प्रेरित गरेको छ। यी सर्पिलहरू मध्ये एक सुनौलो सर्पिल हो, ब्रह्माण्डको वास्तुकलालाई नियन्त्रण गर्ने एक प्रकारको कोड मानिन्छ। सुनौलो सर्पिल एउटा फराकिलो, मनमोहक विषय हो जसले इतिहास र कलाका कार्यहरूमा प्रमुख भूमिका खेलेको छ।
यहाँ सुनौलो सर्पिललाई हेरौं – यसको उत्पत्ति, अर्थ र महत्त्व।
सुनौलो सर्पिल प्रतीक के हो?
गोल्डेन सर्पिल सुनौलो अनुपातको अवधारणामा आधारित बनाइएको एउटा ढाँचा हो—एक विश्वव्यापी नियम जसले जीवन र पदार्थका सबै रूपहरूमा "आदर्श" प्रतिनिधित्व गर्दछ। वास्तवमा, यो प्रायः गणितको नियम र जीवित चीजहरूको संरचना बीचको सम्बन्धको उदाहरणको रूपमा उद्धृत गरिएको छ। हामीले प्रतीकको पछाडिको गणितलाई जति धेरै बुझ्छौं, त्यति नै हामीले प्रकृति र कलामा यसको उपस्थितिको कदर गर्नेछौं।
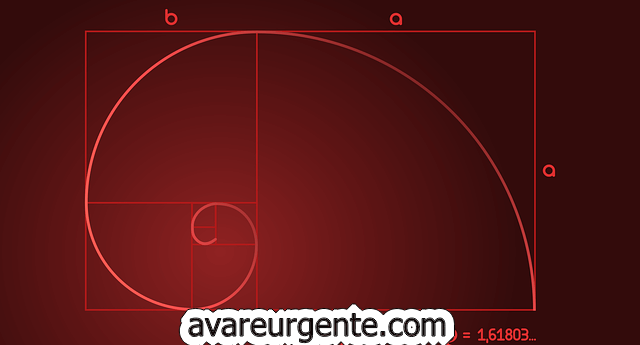
गणितमा, सुनौलो अनुपात एक विशेष संख्या हो जुन लगभग १.६१८ बराबर हुन्छ र ग्रीक अक्षरले प्रतिनिधित्व गर्छ। Φ (Phi)। यो सुनौलो सर्पिल कहाँबाट आयो भनेर तपाईलाई अचम्म लाग्न सक्छ - र यसको जवाफ सुनको आयत भित्र छ। ज्यामितिमा, सुनौलो आयतबाट सुनको सर्पिल कोर्न सकिन्छ जसको पक्षहरू सुनौलो अनुपातमा आनुपातिक हुन्छन्।
1800s मा, जर्मन गणितज्ञ मार्टिन ओमलेविशेष संख्या 1.618 सुनौलो , सम्भवतः किनभने यो सधैं गणितमा अवस्थित छ। समय पछि, यसलाई प्राकृतिक संसारमा यसको आवृत्तिको कारणले दैवी भनेर पनि वर्णन गरिएको थियो। सुनौलो अनुपातबाट बनाइएको सर्पिल ढाँचालाई गोल्डेन सर्पिल पनि भनिन्छ।
गोल्डेन स्पाइरल बनाम फिबोनैकी सर्पिल

सुनौलो अनुपात धेरैमा हुन्छ। गणितीय सन्दर्भहरू। यसैले सुनौलो सर्पिल प्रायः फिबोनाची अनुक्रमसँग सम्बन्धित छ - संख्याहरूको एक श्रृंखला जो फाइसँग नजिक छ। प्राविधिक रूपमा, अनुक्रम 0 र 1 बाट सुरु हुन्छ र असीम रूपमा जारी रहन्छ, र यदि तपाईंले प्रत्येक संख्यालाई यसको पूर्ववर्तीद्वारा विभाजित गर्नुभयो भने, परिणाम सुनौलो अनुपातमा रूपान्तरण हुनेछ, लगभग 1.618।
गणितमा, त्यहाँ धेरै सर्पिल ढाँचाहरू छन् र तिनीहरू मापन गर्न सकिन्छ। सुनौलो सर्पिल र फिबोनाची सर्पिल आकारमा धेरै मिल्दोजुल्दो छन्, र धेरैले तिनीहरूलाई एकै ठाउँमा प्रयोग गर्छन्, तर तिनीहरू समान छैनन्। सबै कुरालाई गणितीय हिसाबले व्याख्या गर्न सकिन्छ, र मापन गर्दा तिनीहरूमा एउटै ठ्याक्कै ढाँचा हुँदैन।
यो भनिन्छ कि फिबोनाची सर्पिलले सुनौलो सर्पिलसँग कुनै निश्चित बिन्दुमा मात्र मेल खान्छ, जब पहिलेको सुनौलो अनुपातमा पुग्छ। वा 1.618। वास्तवमा, फिबोनाची संख्याहरू जति उच्च हुन्छन्, तिनीहरूको सम्बन्ध फाइसँग नजिक हुन्छ। केवल ध्यान राख्नुहोस् कि प्रकृतिमा पाइने हरेक सर्पिल फिबोनाची संख्या वा सुनौलोमा आधारित हुँदैनअनुपात।
गोल्डेन सर्पिलको अर्थ र प्रतीकवाद
सुनौलो सर्पिल प्रतीकले इतिहासभरि अनगिन्ती मानिसहरूलाई प्रेरित गरेको छ। यो जीवन, अध्यात्म र सृष्टिको आधारभूत कुराहरूसँग सम्बन्धित छ।
- जीवन र सृष्टि
गोल्डेन सर्पिल यसको गणितीय गुणहरूमा अद्वितीय छ। र प्रमाणित गर्दछ कि हामी गणितीय नियमहरू द्वारा शासित ब्रह्माण्डमा बस्छौं। जबकि अरूले विश्वास गर्छन् कि यो केवल एक धेरै अनौठो संयोग हो, धेरै वैज्ञानिकहरू र अनुसन्धानकर्ताहरूले यसलाई एक मास्टर गणितज्ञ वा एक सृष्टिकर्ताको प्रमाणको रूपमा मान्दछन्। आखिर, प्रकृतिमा बौद्धिक डिजाइन जटिल छ, र यो संयोगवश आयो भनेर सोच्नु कसैलाई अतार्किक लाग्न सक्छ।
- संतुलन र सद्भाव <1
- The Parthenon <1
- लियोनार्डो दा भिन्चीका चित्रहरू
- गणितमा
- बायोमेकानिक्समा <1
- डिजाइन र कम्पोजिसनमा
- प्रकृतिमा
सुनौलो सर्पिलले गणितज्ञहरू, डिजाइनरहरू र कलाकारहरूको कल्पनालाई आफ्नो सुन्दरताले कब्जा गरेको छ। यो कला र वास्तुकला को केहि महान कार्यहरु मा प्रतिबिम्बित छ। यो सुन्दरतासँग पनि जोडिएको छ, किनकि धेरैले सौन्दर्य गणित र ज्यामितिमा यसको अद्वितीय गुणहरूमा केन्द्रित छ भन्ने विश्वास गर्छन्। केही रहस्यवादीहरू विश्वास गर्छन् कि प्रतीकले व्यक्तिको जीवनमा सन्तुलन र सामंजस्य पनि ल्याउनेछ।
इतिहासमा सुनौलो सर्पिल प्रतीक
सुनौलो सर्पिल प्रतीकको मोहले धेरै कलाकारहरूलाई आफ्नो जीवनमा यसलाई प्रयोग गर्न प्रेरित गरेको छ। उत्कृष्ट कृतिहरू। त्यहाँ राम्रो मौका छ कि तपाईंले पहिले नै प्रतीकलाई विभिन्न कलामा ओभरलेको रूपमा देख्नुभएको छफारमहरू, पार्थेनन देखि मोना लिसा सम्म। दुर्भाग्यवश, यस विषयको बारेमा धेरै भ्रामक दावीहरू छन्, त्यसैले हामी तपाईंलाई ती मिथक वा गणितमा आधारित छ कि छैन भनेर निर्णय गर्न मद्दत गर्नेछौं।

447 र 438 ईसा पूर्वको बीचमा निर्माण गरिएको, एथेन्स, ग्रीसको पार्थेनन अहिलेसम्म बनाइएको सबैभन्दा सौन्दर्यात्मक रूपमा मनमोहक संरचनाहरू मध्ये एक हो। धेरैले यो सुनौलो अनुपातको आधारमा निर्माण भएको अनुमान गरेका छन्। तपाईंले मन्दिरको अगाडिको अनुहारको सुनौलो घुमाउरो र सुनको आयतको साथ धेरै चित्रणहरू पनि देख्नुहुनेछ।
यसमा कुनै शङ्का छैन कि पुरातन ग्रीकहरूले गणित र ज्यामितिलाई उनीहरूको वास्तुकलामा समावेश गरेका थिए, तर विद्वानहरूले गर्न सक्दैनन्। पार्थेनन निर्माणमा सुनौलो अनुपात प्रयोग गरेको ठोस प्रमाण फेला पार्नुहोस्। धेरैजसोले यसलाई मिथक ठान्छन् किनभने धेरैजसो गणितीय प्रमेयहरू मन्दिरको निर्माण पछि मात्र विकसित भएका थिए।
अझ के हो भने, सुनौलो अनुपात र सुनौलो सर्पिल प्रयोग भएको निष्कर्ष निकाल्नको लागि सटीक मापन आवश्यक छ। डिजाइन। विज्ञहरूका अनुसार, सुनको आयत पार्थेनन पुग्ने चरणहरूको आधारमा बनाइनु पर्छ, यसको स्तम्भहरूको आधारमा होइन - सामान्यतया धेरै दृष्टान्तहरूमा देखाइएको छ। साथै, संरचना भग्नावशेषमा छ, जसले यसको सटीक आयामहरूलाई केही अनुमानको अधीनमा बनाउँछ।

लियोनार्डो दा भिन्सीलाई लामो समयदेखि "दैवी" भनिन्छसुनौलो अनुपात संग सम्बन्धित चित्रकार। यस सम्बन्धलाई उपन्यास द दा भिन्ची कोड द्वारा पनि समर्थन गरिएको थियो, किनकि कथानकमा सुनौलो अनुपात र फिबोनाची संख्याहरू समावेश छन्। जबकि सबै कुरा व्याख्याको अधीनमा छ, धेरैले अनुमान गरेका छन् कि चित्रकारले सन्तुलन र सौन्दर्य प्राप्त गर्न जानाजानी आफ्नो काममा सुनौलो सर्पिल प्रयोग गरे। 8> र The Annuciation , तर मोना लिसा वा La Joconde अझै बहसको लागि छ। अन्य दुई चित्रहरूको तुलनामा सन्दर्भ बिन्दुको रूपमा प्रयोग गर्नका लागि केही वास्तु तत्वहरू र सीधा रेखाहरू छन् भनिएको छ। तैपनि, तपाईंले मोना लिसामा सुनौलो अनुपातको धेरै व्याख्याहरू फेला पार्न सक्नुहुन्छ, ओभरलेको रूपमा सुनौलो सर्पिल फिचर गर्दै।
हामीले दा भिन्चीको उत्कृष्ट कृतिहरूका लागि उनको अभिप्राय कहिले पनि थाहा पाउनेछैनौं, तर धेरैले अनौठो संयोगलाई बाध्यकारी ठान्छन्। चित्रकारको पूर्व प्रयोगलाई ध्यानमा राख्दै, यो उसले उक्त चित्रमा पनि प्रयोग गर्नु अप्रत्याशित हुनेछैन। ध्यान राख्नुहोस् कि हरेक दा भिन्सीको चित्रमा सुनौलो अनुपात र सुनौलो सर्पिल समावेश भएको स्पष्ट प्रमाण छैन, त्यसैले उहाँका सबै उत्कृष्ट कृतिहरू तिनीहरूमा आधारित छन् भन्ने निष्कर्षमा पुग्न गाह्रो छ।
गोल्डेन स्पाइरल प्रतीक आधुनिक समय
सुनौलो सर्पिलले जीवन र ब्रह्माण्डको हाम्रो बुझाइमा योगदान गर्छ। यस सम्बन्धमा हालैका केही खोजहरू यहाँ छन्प्रतीक:
सुनौलो सर्पिलले फ्र्याक्टलको ज्यामितिमा भूमिका खेल्छ, जुन सँधै दोहोरिने जटिल ढाँचा हो। अमेरिकी गणितज्ञ एडमन्ड ह्यारिस सुनौलो सर्पिलमा आधारित भग्न वक्रका लागि लोकप्रिय भए, जसलाई अहिले ह्यारिस स्पाइरल भनिन्छ। यो भनिन्छ कि उनले सौन्दर्यको दृष्टिले आकर्षक देखिने ब्रान्चिङ सर्पिलहरू कोर्ने लक्ष्य राखेका थिए, तर उनले गणितीय प्रक्रिया प्रयोग गरेर एक अद्वितीय सर्पिलको साथ समाप्त गरे।
सुनौलो सर्पिलले मानव हातको गतिमा आकर्षक प्रभाव राखेको मानिन्छ। एनाटोमिस्टका अनुसार मानव औंलाहरूको चाल सुनौलो सर्पिलको ढाँचा पछ्याउँछ। तपाईंले ओभरलेको रूपमा सर्पिल प्रतीकको साथ क्लिन्च गरिएको मुट्ठीका छविहरू पनि फेला पार्नुहुनेछ।
आजकल, धेरै डिजाइनरहरूले ओभरले तिनीहरूको कामहरूमा दृश्य सद्भाव प्राप्त गर्ने आशामा यसको सुनौलो अनुपात अनुपात चित्रण गर्न छविमा सुनौलो सर्पिल प्रतीक। केही आधुनिक लोगो र आइकनहरू तिनीहरूमा आधारित छन्, जहाँ डिजाइनरहरूले "अनुपात भित्र अनुपात" को तथाकथित अवधारणा लागू गर्छन्।
प्रकृति घुमाउरो ढाँचाहरूले भरिएको छ तर प्रकृतिमा वास्तविक सुनौलो सर्पिल फेला पार्न दुर्लभ छ। चाखलाग्दो कुरा के छ भने, वैज्ञानिकहरूले पत्ता लगाएका छन् कि बाजहरू आफ्नो शिकारको नजिक पुग्दा सुनौलो घुमाउरो बाटोमा उड्छन्, सम्भवतः यो ऊर्जा-कुशल उडान मार्ग हो।
विपरीतलोकप्रिय विश्वास, नॉटिलस खोल सुनौलो सर्पिल होइन। मापन गर्दा, ती दुईलाई कसरी पङ्क्तिबद्ध वा मापन गरिएको भए पनि मेल खाँदैन। साथै, प्रत्येक नॉटिलस खोल समान रूपमा सिर्जना गरिएको छैन, किनकि प्रत्येकको आकारमा भिन्नता र त्रुटिहरू छन्।
सूर्यमुखी र पाइनकोनका सर्पिलहरू सुन्दर छन्, तर तिनीहरू सुनौलो सर्पिलहरू होइनन्। वास्तवमा, तिनीहरूको सर्पिलहरू सुनको सर्पिलको विपरीत, केन्द्रको वरिपरि लपेट्दैनन्। कतिपय फूलहरूमा फिबोनाची संख्याहरूसँग मिल्दोजुल्दो पंखुडीहरू हुन्छन्, त्यहाँ धेरै अपवादहरू फेला पर्छन्।
विज्ञहरूले यो पनि भन्छन् कि आकाशगंगा वा कहिलेकाहीं आँधीबेहरीको बादल जुन सुनौलो सर्पिलको भागमा फिट हुन्छ भन्ने निष्कर्षमा पुग्नु हुँदैन। कि सबै आकाशगंगाहरू र आँधीहरू सुनौलो अनुपातमा आधारित छन्।
संक्षिप्त रूपमा
हाम्रो ब्रह्माण्ड सर्पिलहरूले भरिएको छ, त्यसैले यो अचम्मको कुरा होइन कि धेरैले तिनीहरूको पछाडिको गणित र तिनीहरूको अर्थमा रुचि राखेका छन्। । कलाकारहरूले लामो समयसम्म सुनको सर्पिललाई आँखाको लागि सबैभन्दा मनमोहक मानेका छन्। यो वास्तवमा प्रकृतिको सबैभन्दा प्रेरणादायक ढाँचा हो जुन रचनात्मक कलात्मक अभिव्यक्तिहरूमा अनुवाद गर्न सकिन्छ।

